
【题目】已知:在平面直角坐标系中,点![]() ,点
,点![]() .
.
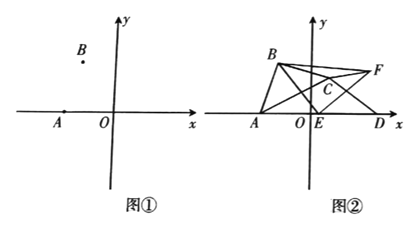
(1)在图①中的![]() 轴上求作点
轴上求作点![]() ,使得
,使得![]() 的值最小;
的值最小;
(2)若![]() 是以
是以![]() 为腰的等腰直角三角形,请直接写出点
为腰的等腰直角三角形,请直接写出点![]() 的坐标;
的坐标;
(3)如图②,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() (不与点
(不与点![]() 重合)是
重合)是![]() 轴上一个动点,点
轴上一个动点,点![]() 是
是![]() 中点,连结
中点,连结![]() ,把
,把![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() (即
(即![]() ,
,![]() ),连结
),连结![]() 、
、![]() 、
、![]() ,试猜想
,试猜想![]() 的度数,并给出证明.
的度数,并给出证明.
【答案】(1)见解析;(2)![]() ,
,![]() ,
,![]() ,
,![]() ;(3)45°,见解析
;(3)45°,见解析
【解析】
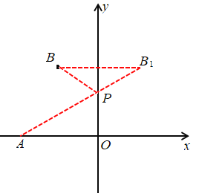
(1)作出点B关于y轴对称的点B1,连接AB1交y轴于点P,则P点即为所求;
(2)分别作出以AB为腰的等腰直角三角形,运用全等三角形的判定与性质求出点C的坐标即可;
(3)分点D运动到点A的右侧和左侧两种情形进行求解:①当点![]() 运动到点
运动到点![]() 右侧时,如图,延长
右侧时,如图,延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,首先证明
,首先证明![]() ≌
≌![]() 即可证明
即可证明![]() 是等腰直角三角形,进而证明
是等腰直角三角形,进而证明![]() ≌
≌![]() 可得
可得![]() ,
,![]() ,从而可得结论;②当点
,从而可得结论;②当点![]() 运动到点
运动到点![]() 左侧时,同理可得.
左侧时,同理可得.
(1)如图所示,
(2) 如图1,过点B作BD⊥x轴于点D,过点C作CE⊥BD于点E,
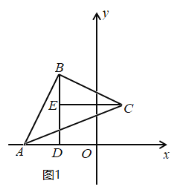
∵∠ABC=90°,
∴∠ABD+∠CBE=90°,
∵∠BAD+∠ABD=90°,
∴∠BAD=∠CBE,
在△BAD和△CBE中,
∴△BAD≌△CBE,
∴BE=AD,CE=BD,
∵A(-3,0),B(-2,3),
∴AD=1,BD=3,OD=2,
∴BE=1,DE=2,
∴C(1,2)
如图2,

易证△BAD≌△ACO,
∴OC=AD=1,
∴C(0,-1);
如图3,
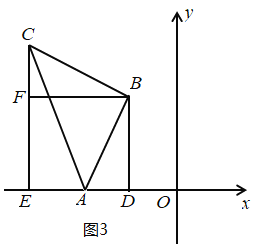
易证△BAD≌△BCF,
∴CF=AD=1,BF=ED=BD=3
∴CE=4,EO=5
∴C(-5,4);
如图4,
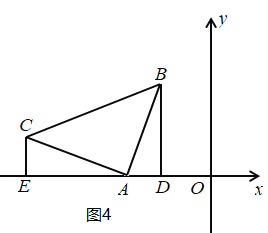
易证△BAD≌△CAE,
∴CE=AD=1,AE= BD=3
∴EO=6
∴C(-6,1);
故点C的坐标为:![]() ,
,![]() ,
,![]() ,
,![]()
(3)猜想![]()
①当点![]() 运动到点
运动到点![]() 右侧时,
右侧时,
如图,延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() ,
,![]()
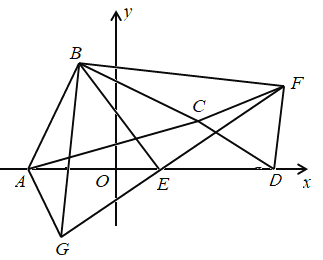
在![]() 和
和![]() 中
中
∵![]() ,
,![]() ,
,![]()
∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
,![]()
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]() ,
,![]() ,
,![]()
∵![]()
∴![]() ,
,
即![]()
∴![]()
在![]() 和
和![]() 中
中
∵![]() ,
,![]() ,
,![]()
∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
,![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
![]() ∵
∵![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形, ![]()
②当点![]() 运动到点
运动到点![]() 左侧时,同理可证,
左侧时,同理可证, ![]()
综上所述, ![]()


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
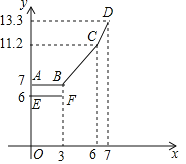
【题目】为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
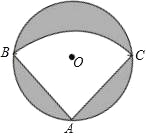
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于![]() 的分式方程
的分式方程![]() .
.
(1)当![]() ,
,![]() 时,求分式方程的解;
时,求分式方程的解;
(2)当![]() 时,求
时,求![]() 为何值时分式方程
为何值时分式方程![]() 无解:
无解:
(3)若![]() ,且
,且![]() 、
、![]() 为正整数,当分式方程
为正整数,当分式方程![]() 的解为整数时,求
的解为整数时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )

A. ①③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() ,点
,点![]() ,若动点
,若动点![]() 从坐标原点出发,沿
从坐标原点出发,沿![]() 轴正方向匀速运动,运动速度为
轴正方向匀速运动,运动速度为![]() ,设点
,设点![]() 运动时间为
运动时间为![]() 秒,当
秒,当![]() 是以
是以![]() 为腰的等腰三角形时,直接写出
为腰的等腰三角形时,直接写出![]() 的所有值__________________.
的所有值__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.

(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com