
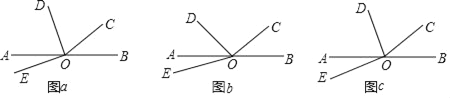
【题目】如图,O为直线AB上一点,∠BOC=α.
(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;
(2)若∠AOD=![]() ∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
(3)若∠AOD=![]() ∠AOC,∠DOE=
∠AOC,∠DOE=![]() (n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
(n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
【答案】(1)20°;(2)∠AOE=![]() α;(3)∠AOE=
α;(3)∠AOE=![]() .
.
【解析】
(1)利用角平分线的性质得出∠AOD=∠DOC=70°,进而得出∠AOE的度数;
(2)利用设∠AOD=x,则∠DOC=2x,∠BOC=180-3x=α,得出x的值,进而用α表示∠AOE的度数;
(3)利用(2)中作法,得出x与α的关系,进而得出答案.
(1)∵∠BOC=40°,OD平分∠AOC,
∴∠AOD=∠DOC=70°,
∵∠DOE=90°,则∠AOE=90°﹣70°=20°;
故答案为:20°;
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180﹣3x=α,
解得:x= ![]() ,
,
∴∠AOE=60﹣x=60﹣![]() =
= ![]() ;
;
(3)设∠AOD=x,则∠DOC=(n﹣1)x,∠BOC=180﹣nx=α,
解得:x=![]() ,
,
∴∠AOE= ![]() ﹣
﹣![]() =
= ![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
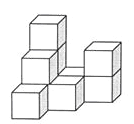
【题目】下图是由几个相同的小正方体搭成的几何体,
(1)搭成这个几何体需要 个小正方体;
(2)画出这个几何体的主视图和左视图;
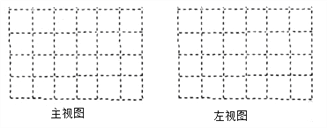
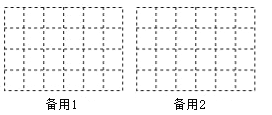
(3)在保持主视图和左视图不变的情况下,最多可以拿掉n个小正方体,则n= ,请在备用图中画出拿掉n个小正方体后新的几何体的俯视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2018的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出点A′,B′,C′的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C都是格点.
(1)将△ABC向左平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2;
(3)作出△ABC关于直线l对称的△A3B3C3,使A,B,C的对称点分别是A3,B3,C3;
(4)△A2B2C2与△A3B3C3成______________△A1B1C1与△A2B2C2成_____________(填“中心对称”或“轴对称”).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=x2+2x﹣3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(﹣4,0),与y轴交于点D(0,2).
(1)求抛物线C2的解析式;
(2)设点P为线段AB上一动点(点P不与点A,B重合),过点P作x轴的垂线交抛物线C1于点M,交抛物线C2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.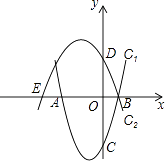
查看答案和解析>>
科目:初中数学 来源: 题型:
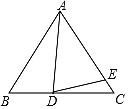
【题目】如图所示,已知在△ABC中,AB=AC,D为线段BC上一点,E为线段AC上一点,且AD=AE.
(1)若∠ABC=60°,∠ADE=70°,求∠BAD与∠CDE的度数;
(2)设∠BAD=α,∠CDE=β,试写出α、β之间的关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ).
![]()
A. 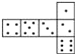 B.
B. 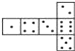 C.
C.  D.
D. 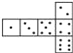
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com