
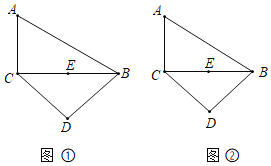
【题目】已知![]() 中,
中,![]() 点
点![]() 为
为![]() 的中点,以
的中点,以![]() 为底边的等腰
为底边的等腰![]() 按如图所示位置摆放,且
按如图所示位置摆放,且![]() .请仅用无刻度的直尺分别按下列要求作图(保留作图痕迹).
.请仅用无刻度的直尺分别按下列要求作图(保留作图痕迹).
![]() 如图①,在
如图①,在![]() 上求作一点
上求作一点![]() ,使四边形
,使四边形![]() 为菱形;
为菱形;
![]() 如图②,过点
如图②,过点![]() 作线段
作线段![]() 使得线段
使得线段![]() 将
将![]() 的面积平分.
的面积平分.
【答案】(1)作图见解析
(2)作图见解析
【解析】
(1)延长DE交AB于F,利用△BDC为等腰三角形,E为BC的中点,则DF垂直平分BC,再根据∠DBC=∠ABC得到BF=BD,所以BE垂直平分DF,然后根据菱形的判定方法得到四边形BDCF为菱形;
(2)由(1)得到CD为斜边上的中线,连接AE交CD于点O,则点O为△ABC的重心,连接BO并延长交AC于Q,则Q点为AC的中点,延长QE交BD于P,则CP为BD边的中线,线段CP将△BCD的面积平分.
(1)延长DE交AB于F,如图![]() 点
点![]() 即为所求;
即为所求;
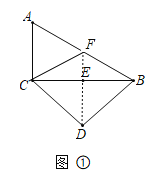
(2)连接AE交CD于点O,连接BO并延长交AC于Q,延长QE交BD于P,线段CP将△BCD的面积平分.如图![]() 线段
线段![]() 即为所求.
即为所求.



科目:初中数学 来源: 题型:
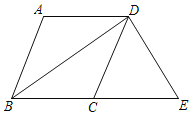
【题目】如图,面积为24的ABCD中,对角线BD平分∠ABC,过点D作DE⊥BD交BC的延长线于点E,DE=6,则sin∠DCE的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的项点为
的项点为![]() ,交
,交![]() 轴于
轴于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧),且
点左侧),且![]() .
.
(1)求抛物线![]() 的函数解析式;
的函数解析式;
(2)过点![]() 的直线交抛物线于点
的直线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 的面积被
的面积被![]() 轴分为1: 4两个部分,求直线
轴分为1: 4两个部分,求直线![]() 的解析式;
的解析式;
(3)在(2)的情况下,将抛物线![]() 绕点
绕点![]() 逆时针旋转180°得到抛物线
逆时针旋转180°得到抛物线![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,当点
上一点,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 为直角三角形?
为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD的对角线交于点O,AC=2BD,点P是AO上一个动点,过点P作AC的垂线交菱形的边于M,N两点.设AP=x,△OMN的面积为y, 表示y与x的函数关系的图象大致如图2所示,则菱形的周长为

A. 2 B. ![]() C. 4 D.
C. 4 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
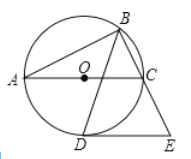
(1)若∠BAC=28°20′,则∠E= ;
(2)求证:DE是⊙O的切线;
(3)若tan∠ACB=2 ,BC=2![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com