

分析 (1)先根据网格求得AB、BC、CD三条线段的长,再相加求得所走的路程的近似值;
(2)根据要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复,进行作图即可.
解答 解:(1)根据图1可得:$AB=\sqrt{{2^2}+{4^2}}=2\sqrt{5}$,$BC=\sqrt{{2^2}+{1^2}}=\sqrt{5}$,CD=3
∴A站到B站的路程=$AB+BC+CD=2\sqrt{5}+\sqrt{5}+3=3+3\sqrt{5}$≈9.7;
(2)从A站到D站的路线图如下:
点评 本题主要考查了作图,解决问题的关键是掌握勾股定理以及图形的基本变换.在作图时要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
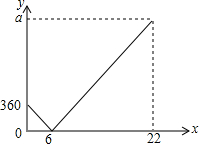 小明家、小芳家与人民公园依次在一条直线上,小明、小芳两人同时各自从家沿直线匀速步行到人民公园,已知小明到达公园花了22分钟,小芳的步行速度是40米/分钟,设两人出发x(分钟)后,小明离小芳家的距离为y(米),y与x的函数关系如图所示.
小明家、小芳家与人民公园依次在一条直线上,小明、小芳两人同时各自从家沿直线匀速步行到人民公园,已知小明到达公园花了22分钟,小芳的步行速度是40米/分钟,设两人出发x(分钟)后,小明离小芳家的距离为y(米),y与x的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com