



科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 △ADC除外);
△ADC除外);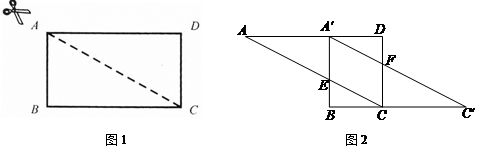
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省高邮市九年级中考模拟数学试卷(解析版) 题型:解答题
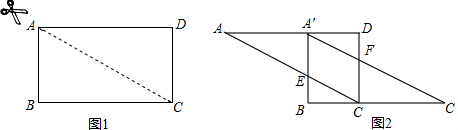
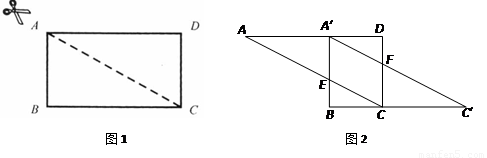
将图1中的矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图2中的△A′BC′
1.写出图2中的两对全等的三角形(不能添加辅助线和字母,△C′BA′ △ADC除外);
△ADC除外);
2.选择一对加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com