
【题目】如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.
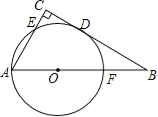
(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.
(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.
【答案】(1)证明见解析;(2)![]() ;3
;3![]() .
.
【解析】试题(1)连接OD、OE、ED.先证明△AOE是等边三角形,得到AE=AO=0D,则四边形AODE是平行四边形,然后由OA=OD证明四边形AODE是菱形;
(2)连接OD、DF.先由△OBD∽△ABC,求出⊙O的半径,然后证明△ADC∽△AFD,得出AD2=ACAF,进而求出AD.
试题解析:(1)证明:如图1,连接OD、OE、ED.
∵BC与⊙O相切于一点D,
∴OD⊥BC,
∴∠ODB=90°=∠C,
∴OD∥AC,
∵∠B=30°,
∴∠A=60°,
∵OA=OE,
∴△AOE是等边三角形,
∴AE=AO=0D,
∴四边形AODE是平行四边形,
∵OA=OD,
∴四边形AODE是菱形.
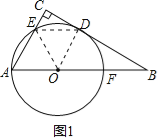
(2)解:设⊙O的半径为r.
∵OD∥AC,
∴△OBD∽△ABC.
∴![]() ,即8r=6(8﹣r).
,即8r=6(8﹣r).
解得r=![]() ,
,
∴⊙O的半径为![]() .
.
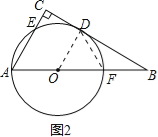
如图2,连接OD、DF.
∵OD∥AC,
∴∠DAC=∠ADO,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠DAC=∠DAO,
∵AF是⊙O的直径,
∴∠ADF=90°=∠C,
∴△ADC∽△AFD,
∴![]() ,
,
∴AD2=ACAF,
∵AC=6,AF=![]() ,
,
∴AD2=![]() ×6=45,
×6=45,
∴AD=![]() =3
=3![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() ,
,![]() 两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到
两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到![]() 地,乙车立即以原速原路返回到
地,乙车立即以原速原路返回到![]() 地.甲、乙两车距B地的路程
地.甲、乙两车距B地的路程![]() (
(![]() )与各自行驶的时间
)与各自行驶的时间![]() (
(![]() )之间的关系如图所示.
)之间的关系如图所示.
(1)求甲车距![]() 地的路程
地的路程![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求乙车距![]() 地的路程
地的路程![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当甲车到达![]() 地时,乙车距
地时,乙车距![]() 地的路程为
地的路程为 ![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC,AB于点E,F.
(1)若∠B=30°,求证:以A,O,D,E为顶点的四边形是菱形;
(2)填空:若AC=6,AB=10,连接AD,则⊙O的半径为 ,AD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),经过第2019次变换后所得的点A的坐标是( )
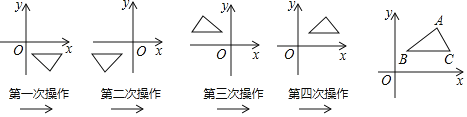
A.(﹣a,b)B.(﹣a,﹣b)C.(a,﹣b)D.(a,b)
查看答案和解析>>
科目:初中数学 来源: 题型:
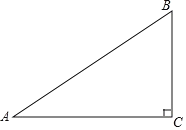
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
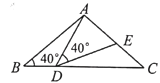
【题目】如图, ![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .以下四个结论:
.以下四个结论:
①![]() ;
;
②当![]() 为
为![]() 中点时
中点时![]() ;
;
③当![]() 时
时![]() ;
;
④当![]() 为等腰三角形时
为等腰三角形时![]() .
.
其中正确的结论是_________(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如图1,![]() 中,点
中,点![]() ,
,![]() 在边
在边![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,求证:
,求证:![]() .
.
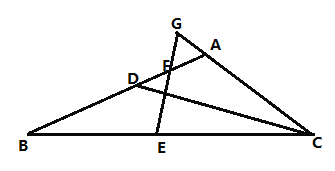
等腰三角形是一种常见的轴对称图形,几何试题中我们常将一腰所在的三角形沿着等腰三角形的对称轴进行翻折,从而构造轴对称图形.
①小明的想法是:将![]() 放到
放到![]() 中,沿等腰
中,沿等腰![]() 的对称轴进行翻折,即作
的对称轴进行翻折,即作![]() 交
交![]() 于
于![]() (如图2)
(如图2)
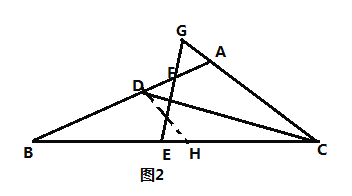
②小白的想法是:将![]() 放到
放到![]() 中,沿等腰
中,沿等腰![]() 的对称轴进行翻折,即作
的对称轴进行翻折,即作![]() 交
交![]() 的延长线于
的延长线于![]() (如图3)
(如图3)
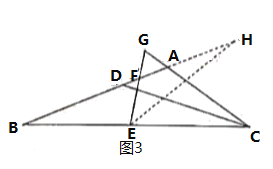
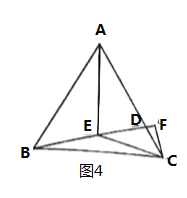
经验拓展:等边![]() 中,
中,![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长(用含
的长(用含![]() ,
,![]() 的式子表示).
的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com