
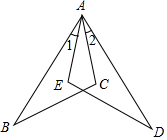
 如图所示,已知∠1=∠2,AC=AE,再添一个条件AB=AD或∠B=∠D或∠C=∠E,使△ABC≌△ADE.(只需写出一个即可)
如图所示,已知∠1=∠2,AC=AE,再添一个条件AB=AD或∠B=∠D或∠C=∠E,使△ABC≌△ADE.(只需写出一个即可) 分析 先根据∠1=∠2,等号两边都加上∠EAC,得到∠BAC=∠DAE,由已知AC=AE,要使△ABC≌△ADE,根据全等三角形的判定:添上AB=AD,根据有两边及夹角相等的两个三角形全等(简称SAS);添上∠B=∠D,根据有两角及其夹边对应相等的两个三角形全等(AAS);添上∠C=∠E,根据有两边及其夹角对应相等的两个三角形全等(ASA).
解答 解:可补充的条件是:
当AB=AD,△ABC≌△ADE(SAS);
当∠B=∠D,△ABC≌△ADE(ASA);
当∠C=∠E,△ABC≌△ADE(AAS).
故答案为:AB=AD或∠B=∠D或∠C=∠E.
点评 本题考查了全等三角形的判定;题目是开放型题目,根据已知条件结合判定方法,找出所需条件,一般答案不唯一,只要符合要求即可.


科目:初中数学 来源: 题型:选择题
| A. | -1<-5<0<1 | B. | -5<-1<0<1 | C. | 1<0<-1<-5 | D. | 0<-5<-1<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
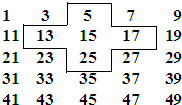 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
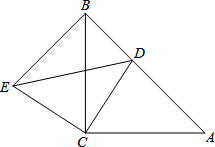 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上,连接BE.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )
如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )| A. | 8 | B. | 21 | C. | 14 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com