
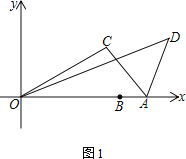
【题目】已知,点A(8,0)、B(6,0).将线段OB绕着原点O逆时针方向旋转角度α到OC,连接AC.将AC绕着点A顺时针方向旋转角度β至AD,连接OD
(1)当α=30°,β=60°时,求OD的长
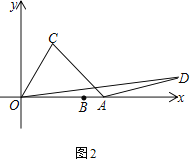
(2)当α=60°,β=120°时,求OD的长
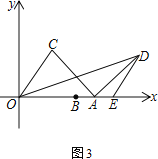
(3)已知E(10,0),当β=90°时,改变的大小,求ED的最大值
【答案】(1)![]() ;(2)
;(2)![]() ;(3)最大值为
;(3)最大值为![]()
【解析】
(1)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() ,再证明
,再证明![]() 后利用勾股定理求解即可;
后利用勾股定理求解即可;
(2)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() ,所以
,所以![]() .再证明
.再证明![]() ,利用勾股定理即可求出
,利用勾股定理即可求出![]() ;
;
(3)将![]() 绕
绕![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,可得点N(8,8),利用两点间的距离公式可求出
,可得点N(8,8),利用两点间的距离公式可求出![]() ,当点D在线段NE上时,DE有最小值
,当点D在线段NE上时,DE有最小值![]() ,当D在线段NE的延长线上时,DE有最大值,最大值为
,当D在线段NE的延长线上时,DE有最大值,最大值为![]() .
.
解:(1)如图,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,
,
则![]() 是等边三角形,
是等边三角形,
∴![]()
∴![]()
∴![]() ,即
,即![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]() ;
;
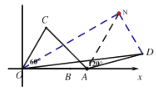
(2)如图,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 是等边三角形,
是等边三角形,
∵![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵∵![]()
∴![]()
∴![]() ;
;
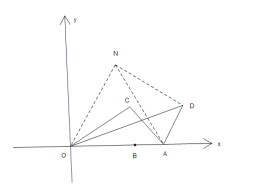
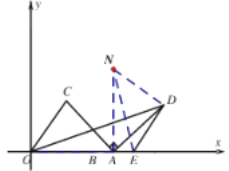
(3)如图,将![]() 绕
绕![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接AN、DN、EN,可得点N(8,8),
,连接AN、DN、EN,可得点N(8,8),
则![]()
由(1)得,![]()
∴![]()
∴当点D在线段NE上时,DE有最小值,最小值为:![]() ;
;
当D在线段NE的延长线上时,DE有最大值,最大值为:![]() ;
;
∴DE最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生每月的零用钱情况,从甲、乙、丙三个学校各随机抽取200名学生,调查了他们的零用钱情况(单位:元)具体情况如下:
学校频数零用钱 | 100≤x<200 | 200≤x<300 | 300≤x<400 | 400≤x<500 | 500以上 | 合计 |
甲 | 5 | 35 | 150 | 8 | 2 | 200 |
乙 | 16 | 54 | 68 | 52 | 10 | 200 |
丙 | 0 | 10 | 40 | 70 | 80 | 200 |
在调查过程中,从__(填“甲”,“乙”或“丙”)校随机抽取学生,抽到的学生“零用钱不低于300元”的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形 ABCD 内接于⊙O,连接 AC、BD,∠BAD+2∠ACB=180°.
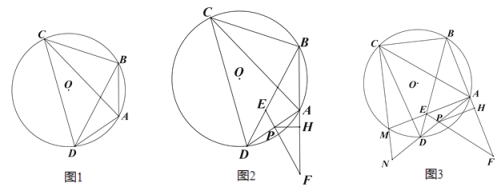
(1)如图 1,求证:点 A 为弧 BD 的中点;
(2)如图 2,点 E 为弦 BD 上一点,延长 BA 至点 F,使得 AF=AB,连接 FE 交 AD 于点 P,过点 P 作 PH⊥AF 于点 H,AF=2AH+AP,求证:AH:AB=PE:BE;
(3)在(2)的条件下,如图 3,连接 AE,并延长 AE 交⊙O 于点 M,连接 CM,并延长 CM 交 AD 的延长线于点 N,连接 FD,∠MND=∠MED,DF=12﹒sin∠ACB,MN=![]() ,求 AH 的长.
,求 AH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货价为30元的书包以40元售出,平均每月能售出600个,调查表明:这种书包的售价每上涨1元,其销售量就减少10个.
(1)为了使平均每月有10000元的销售利润,这种书包的售价应定为多少元?
(2)10000元的利润是否为最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时书包的售价为多少元?
(3)请分析并回答售价在什么范围内商家就可以获得利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
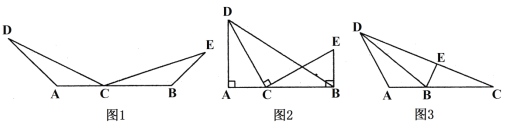
【题目】⑴如图1,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE,DC=CE.求证:AC=BE.
⑵如图2,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE=90°.
①求证:![]() ;②连接BD,若∠ADC=∠ABD,AC=3,BC=
;②连接BD,若∠ADC=∠ABD,AC=3,BC=![]() ,求tan∠CDB的值;
,求tan∠CDB的值;
⑶如图3,在△ABD中,点C在AB边上,且∠ADC=∠ABD,点E在BD边上,连接CE,∠BCE+∠BAD=180°,AC=3,BC=![]() ,CE=
,CE=![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC+∠BEA=( )
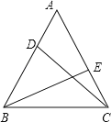
A.180°B.170°C.160°D.150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com