
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,点D是AB中点,过点D作DF⊥AC,垂足为F,过点C作AB的平行线,交DF的延长线于点E,连接CD,AE.
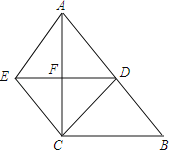
(1)求证:四边形AECD是菱形;
(2)当∠BAC的大小满足什么条件时,四边形AECD是正方形?证明你的结论.
【答案】(1)见解析;(2)当∠BAC=45°时,四边形AECD是正方形;理由见解析
【解析】
试题分析:(1)由ASA证明△CEF≌△ADF,得出对应边相等EF=DF,证出四边形AECD是平行四边形,再由对角线互相垂直,即可得出四边形AECD是菱形;
(2)由菱形的性质得出∠EAC=∠BAC=45°,得出∠EAD=90°,即可得出四边形AECD是正方形.
(1)证明:∵∠ACB=90°,DF⊥AC,
∴DF∥BC,∵点D是AB中点,
∴F是AC的中点,
∴AF=CF,
∵CE∥AB,
∴∠ECF=∠DAF,
在△CEF和△ADF中,
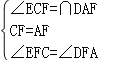 ,
,
∴△CEF≌△ADF(ASA),
∴EF=DF,
∴四边形AECD是平行四边形,
又∵DF⊥AC,
∴四边形AECD是菱形;
(2)解:当∠BAC=45°时,四边形AECD是正方形;理由如下:
∵四边形AECD是菱形,
∴∠EAC=∠BAC=45°,
∴∠EAD=90°,
∴四边形AECD是正方形.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】下列语句正确的是( )
A. 如果一个数的立方根是这个数本身,那么这个数一定是0
B. 一个数的立方根不是正数就是负数
C. 负数没有立方根
D. 一个不为零的数的立方根和这个数同号,0的立方根是0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是( )
A.开口向上,顶点坐标为(﹣1,﹣4) B.开口向下,顶点坐标为(1,4)
C.开口向上,顶点坐标为(1,4) D.开口向下,顶点坐标为(﹣1,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个多边形的每个内角都等于150°,则这个多边形是边形.
B.用计算器计算:sin15°32'(精确到0.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com