
 如图,15个外径为1m的钢管以如图方式堆放,为了防雨,需要搭建防雨棚的高度最低应为( )m.
如图,15个外径为1m的钢管以如图方式堆放,为了防雨,需要搭建防雨棚的高度最低应为( )m.A、2
| ||||
B、
| ||||
| C、5 | ||||
D、2
|
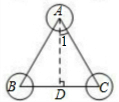 由题意可知:等边△ABC的边长AC=BC=4,
由题意可知:等边△ABC的边长AC=BC=4,| 1 |
| 2 |
| 1 |
| 2 |
| AC2-DC2 |
| 42-22 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
| a2-b2+2b-1 |
| a2-b2+a+b |
| A、2012 | ||
| B、2011 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 评委 | 一号 | 二号 | 三号 | 四号 | 五号 | 六号 | 七号 |
| 评分 | 9.2 | 9.8 | 9.6 | 9.5 | 9.6 | 9.4 | 9.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 班级学生数 | 配备教师数 | 硬件建设(万元) | 教师年薪(万元) | |
| 初中 | 50 | 2.0 | 28 | 1.2 |
| 高中 | 40 | 2.5 | 58 | 1.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com