Question

在四边形ABCD中，对角线AC、BD相交于点O，从（1）OA=OC；（2）OB=OD；（3）AB=CD；（4）AB∥CD；（5）AC平分∠BAD；（6）AC⊥BD这六个条件中，任意选取三个条件推出四边形ABCD是菱形，如（1）（2）（6）?ABCD是菱形，再写出符合要求的两种情况：______?ABCD是菱形；______?ABCD是菱形．

Answer 1

答：（3）（4）（6）?ABCD是菱形．
证明：∵AB=CD，AB∥CD，
∴四边形ABCD平行四边形，
∵AC⊥BD，
∴四边形ABCD是菱形．

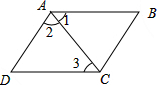
（3）（4）（5）?ABCD是菱形．
∵AB=CD，AB∥CD，
∴四边形ABCD平行四边形，∠1=∠3，
∵AC平分∠BAD，
∴∠1=∠2，
∴∠2=∠3，
∴AD=CD，
∴四边形ABCD是菱形．
故答案为：（3）（4）（6）；（3）（4）（5）．
分析：由（3）（4），可证得四边形ABCD是平行四边形，又由AC⊥BD，即可证得四边形ABCD是菱形．
由（3）（4），可证得四边形ABCD是平行四边形，又由AC平分∠BAD，即可证得△ACD是等腰三角形，继而证得四边形ABCD是菱形．
点评：此题考查了菱形的判定以及等腰三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．