
【题目】如图,在△ABC 中,AB=AC,点D,E在边BC上,且BD=CE.
(1)求证: △ABD≌△ACE;
(2)若∠B=40°,AB=BE,求∠DAE的度数.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大黄鱼是中国特有的地方性鱼种类,有“国鱼”之称.由于过去滥捕等多种因素,大黄鱼资源已基本枯竭.目前,我市已培育出十余种大黄鱼品种.某鱼苗人工养殖基地对其中的四个品种“宁港”、“御龙”、“甬岱”、“象山港”共300尾鱼苗进行成活实验,从中选出成活率最高的品种进行推广.通过实验得知“甬岱”品种鱼苗成活率为80%,并把实验数据绘制成下列两幅统计图(部分信息未给出):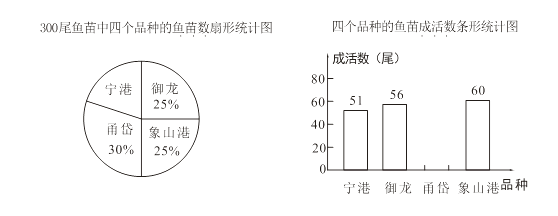
(1)求实验中“宁港”品种鱼苗的数量;
(2)求实验中“甬岱”品种鱼苗的成活数,并补全条形统计图;
(3)你认为应选哪一品种进行推广?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行.本届论坛期间,中国同30多个国家签署经贸合作协议.某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区.已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点 ![]() 出发,在矩形
出发,在矩形 ![]() 边上沿着
边上沿着 ![]() 的方向匀速移动,到达点
的方向匀速移动,到达点 ![]() 时停止移动.已知机器人的速度为
时停止移动.已知机器人的速度为 ![]() 个单位长度/
个单位长度/ ![]() ,移动至拐角处调整方向需要
,移动至拐角处调整方向需要 ![]()
![]() (即在
(即在 ![]() 、
、 ![]() 处拐弯时分别用时
处拐弯时分别用时 ![]()
![]() ).设机器人所用时间为
).设机器人所用时间为 ![]() 时,其所在位置用点
时,其所在位置用点 ![]() 表示,
表示, ![]() 到对角线
到对角线 ![]() 的距离(即垂线段
的距离(即垂线段 ![]() 的长)为
的长)为 ![]() 个单位长度,其中
个单位长度,其中 ![]() 与
与 ![]() 的函数图像如图②所示.
的函数图像如图②所示.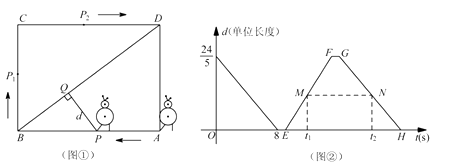
(1)求 ![]() 、
、 ![]() 的长;
的长;
(2)如图②,点 ![]() 、
、 ![]() 分别在线段
分别在线段 ![]() 、
、 ![]() 上,线段
上,线段 ![]() 平行于横轴,
平行于横轴, ![]() 、
、 ![]() 的横坐标分别为
的横坐标分别为 ![]() 、
、 ![]() .设机器人用了
.设机器人用了 ![]() 到达点
到达点 ![]() 处,用了
处,用了 ![]() 到达点
到达点 ![]() 处(见图①).若
处(见图①).若 ![]() ,求
,求 ![]() 、
、 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= ![]() x的图象与反比例函数y=
x的图象与反比例函数y= ![]() 的图象交于A(a,﹣2),B两点.
的图象交于A(a,﹣2),B两点. 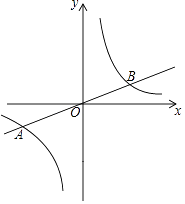
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com