
分析 (1)直接根据题意先求出增加的租金是4个5000,从而计算出租出多少间;
(2)设每间商铺的年租金增加x万元,直接根据收益=租金-各种费用=275万元作为等量关系列方程求解即可.
解答 解:(1)∵(130000-100000)÷5000=6,
∴能租出30-6=24(间).
(2)设每间商铺年租金增加x万元
所以(30-$\frac{x}{05}$)(10+x)-(30-$\frac{x}{0.5}$)×1-$\frac{x}{0.5}$×0.5=275,
解得x1=5,x2=0.5,
∴每间商铺的年租金为10.5万元或15万元
∴若从减少空铺的角度来看,当每间商铺的年租金为10.5万元时,该公司的年收益为275万元.
点评 此题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题中的等量关系题目中已经给出,相对降低了难度.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
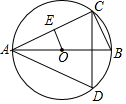 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
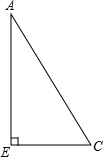 已知Rt△AEC中,∠E=90°,请按如下要求进行操作和判断:
已知Rt△AEC中,∠E=90°,请按如下要求进行操作和判断:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com