【题目】下列各组数据中，能构成三角形的是（ ）
A. 1、2、3 B. 2、3、4 C. 4、9、4 D. 2、1、4
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案科目：初中数学 来源： 题型：
【题目】若关于x的一元二次方程为ax2+bx+5=0（a≠0）的解是x=1，则2013﹣a﹣b的值是（ ）
A.2 018
B.2 008
C.2 014
D.2 012
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．求：
（1）∠BAE的度数；
（2）∠DAE的度数；
（3）探究：小明认为如果条件∠B=70°，∠C=30°改成∠B-∠C=40°，也能得出∠DAE的度数？若能，请你写出求解过程；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD为△ABC的中线，BE为△ABD的中线．
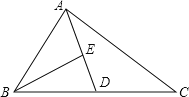
（1）∠ABE=15°，∠BAD=40°，求∠BED的度数；
（2）在△BED中作BD边上的高；
（3）若△ABC的面积为40，BD=5，则点E到BC边的距离为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：配方法是中学数学的重要方法，用配方法可求最大（小）值。如对于任意正实数
、x，可作变形：x+=（－
）2+2，因为（－）2≥0，所以x+≥2（当x=时取等号）．
记函数y=x+（a＞0，x＞0），由上述结论可知：当x=时，该函数有最小值为2．
直接应用： 已知函数y1=x（x＞0）与函数y2 = （x＞0），则当x= 时，y1+y2取得最小值为 ．
变形应用： 已知函数y1=x+1（x＞-1）与函数y2=（x+1）2+4（x＞-1），求 的最小值，并指出取得该最小值时相应的x的值．
实际应用：汽车的经济时速是指汽车最省油的行驶速度。某种汽车在每小时70～110公里之间行驶时（含70公里和110公里），每公里耗油（+）升。若该汽车以每小时x公里的速度匀速行驶，1小时的耗油量为y升．
①、求y关于x的函数关系式（写出自变量x的取值范围）；
②、求该汽车的经济时速及经济时速的百公里耗油量（结果保留小数点后一位）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校九年级（1）班所有学生参加
年初中毕业生升学体育测试，根据测试评分标准，将他们的成绩进行统计后分为
、
、
、
四等，并绘制成如图所示的条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题：
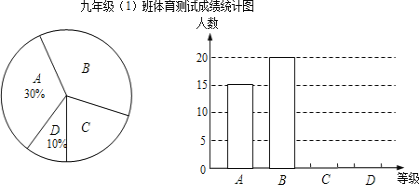
（1）九年级（1）班参加体育测试的学生有 人；
（2）将条形统计图补充完整；
（3）在扇形统计图中，等级
部分所占的百分比是 ，等级
对应的圆心角的度数为 ；
（4）若该校九年级学生共有850人参加体育测试，估计达到
级和
级的学生共有 人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市地铁一号与地铁二号线接通后，该市交通通行和转换能力成倍增长，该工程投资预算约为930000万元，这一数据用科学记数法表示为（ ）
A.9.3×105万元
B.9.3×106万元
C.0.93×106万元
D.9.3×104万元
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于任意三角形的高，下列说法不正确的是（ ）
A. 直角三角形只有一条高
B. 锐角三角形有三条高
C. 任意三角形都有三条高
D. 钝角三角形有两条高在三角形的外部
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
