
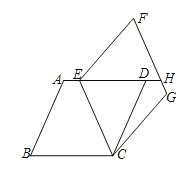
【题目】如图,完全相同的两个菱形ABCD和ECGF的顶点C重合,∠B=∠F,点E恰好在边AD上,延长ED交FG于点H.
(1)求证:∠B=∠ECB;
(2)连接BE、CH.
①试判断四边形BEHC的形状,并说理理由;
②求证:CH平分∠DCG.
【答案】(1)证明见解析,(2)①四边形BEHC是平行四边形,理由见解析,②证明见解析.
【解析】
(1)过A作AN![]() BC于N,作EM
BC于N,作EM![]() BC于M,利用菱形的性质,证明
BC于M,利用菱形的性质,证明![]() 即可得到结论,
即可得到结论,
(2)①利用菱形的性质与∠B=∠F,证明![]() 即可得到结论,
即可得到结论,
②延长BC交FG的延长线于K,证明四边形![]() 是菱形,再证明
是菱形,再证明![]() 利用菱形的性质证明
利用菱形的性质证明![]() 再利用三角形的内角和可得结论.
再利用三角形的内角和可得结论.
证明:(1)如图,过A作AN![]() BC于N,作EM
BC于N,作EM![]() BC于M,
BC于M,
![]() 完全相同的两个菱形ABCD和ECGF,
完全相同的两个菱形ABCD和ECGF,
![]()
![]()
![]()
![]()

(2)①四边形BEHC是平行四边形,理由如下:
如图,连接BE,CH,
![]() 完全相同的两个菱形ABCD和ECGF,
完全相同的两个菱形ABCD和ECGF,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形BEHC是平行四边形
四边形BEHC是平行四边形

②如图,延长BC交FG的延长线于K,
![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() 四边形
四边形![]() 是菱形,
是菱形,
![]()
![]()
![]()
![]()
![]()
![]() 完全相同的两个菱形ABCD和ECGF,
完全相同的两个菱形ABCD和ECGF,
![]()
![]()
![]()
![]()
![]() 平分
平分![]()



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
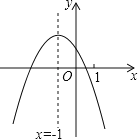
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下所示两幅不完整的统计图,请结合图中所给信息,解答下列问题:

(1)本次调研活动共调研了 名学生,表示“QQ”的扇形圆心角的度数是 度.
(2)请你补充完整条形统计图;
(3)如果该校有2500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在相邻两点距离为1的点阵纸上(左右相邻或上下相邻的两点之间的距离都是1个单位长度),三个顶点都在点阵上的三角形叫做点阵三角形,请按要求完成下列操作:

(1)将点阵△ABC水平向右平移4个单位长度,再竖直向上平移5个单位长度,画出平移后的△A1B1C1;
(2)连接AA1、BB1,则线段AA1、BB1的位置关系为 、数量关系为 .估计线段AA1的长度大约在 <AA1< 单位长度:(填写两个相邻整数);
(3)画出△ABC边AB上的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨 | 频数 | 频率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合计 | d | 1.00 |

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】响应“家电下乡”的惠农政策,某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台,其中甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132 000元.已知甲、乙、丙三种电冰箱的出厂价格分别为:1 200元/台、1 600元/台、2 000元/台
(1)至少购进乙种电冰箱多少台?
(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数,则有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
已知:如图,∠D=110°,∠EFD=70°,∠1=∠2,
求证:∠3=∠B

证明:∵∠D=110°, ∠EFD=70°(已知)
∴∠D+∠EFD=180°
∴AD∥______( )
又∵∠1=∠2(已知)
∴_____∥BC ( 内错角相等,两直线平行)
∴EF∥_____ ( )
∴∠3=∠B(两直线平行,同位角相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个函数y与自变量x的部分对应值如下表:

(1)从我们已学过的函数判断:y是x的 函数,y与x的函数关系式为 ;
(2)根据函数图像,当-2 x -![]() 时,求y的取值范围.
时,求y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com