
ЁОЬтФПЁПХзЮяЯпyЃНЉ![]() +bx+cНЛxжсИКАыжсгкЕуAЃЌНЛyжсе§АыжсгкЕуBЃЌжБЯпABЕФНтЮіЪНЮЊyЃН
+bx+cНЛxжсИКАыжсгкЕуAЃЌНЛyжсе§АыжсгкЕуBЃЌжБЯпABЕФНтЮіЪНЮЊyЃН![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓbЃЌcЕФжЕЃЛ
ЃЈ2ЃЉBAбиyжсЗел180ЁуЕУЕНBAЁфЃЌFЮЊAЁфBЩЯвЛЕуЃЌBFЕФДЙжБЦНЗжЯпНЛyжсгкЕуLЃЌRЮЊxжсЩЯвЛЕуЃЌBF+ORЃН2ЃЌQRЁЭFLгкQЃЌЧѓQRЕФГЄЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌжБЯпLFНЛxжсгкЕуDЃЌEЮЊХзЮяЯпЕквЛЯѓЯоЩЯвЛЕуЃЌBEЃНBDЃЌЁЯABE+ЁЯABDЃН180ЁуЃЌЧѓЕуEЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉbЃН![]() ЃЌcЃН2
ЃЌcЃН2![]() ЃЛЃЈ2ЃЉQR=ЃН2ЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉQR=ЃН2ЃЛЃЈ3ЃЉ![]() Лђ
Лђ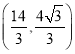
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіAЁЂBзјБъдйДњШыХзЮяЯпНтЮіЪНМДПЩЫуГіbЁЂcЃЎ
ЃЈ2ЃЉЩшLQбгГЄЯпНЛxжсгкЕуDЃЌгЩЬтвтПЩжЊLBЃНLFЃЌДгЖјПЩШЗЖЈЁЯDLOЃН60ЁуЃЌвђДЫжЛашЧѓRDЕФГЄЖШОЭПЩвдСЫЃЌИљОнЩшЖјВЛЧѓЕФЫМЯыЃЌЩшBLЃНLFЃНmЃЌЗжБ№БэЪОГіOLЁЂODЁЂORГЄЖШЃЌODЉORМДЪЧRDЕФГЄЖШЃЌЖјQRЪЧRDЕФвЛАыЃЎ
ЃЈ3ЃЉгЩЁЯABE+ЁЯABDЃН180ЁувдМАBEЃНBDПЩвдЕМГіABЁЮDEЃЌзїBPЁЭABНЛxжсгкЕуPЃЌСЌНгEPЃЌПЩжЄЕУЁїEDPЪЧЕШБпШ§НЧаЮЃЌЩшDЕуКсзјБъЮЊnЃЌдђПЩНЋEЕузјБъгУnБэЪОГіРДЃЌдйНЋEЕузјБъДњШыХзЮяЯпНтЮіЪНМДПЩЧѓГіnЕФжЕЃЌвВОЭЧѓГіСЫEЕузјБъЃЎ
ЃЈ1ЃЉЁпжБЯпyЃН![]() x+2
x+2![]() ЗжБ№гыxжсЁЂyжсНЛгкAЁЂBСНЕуЃЌ
ЗжБ№гыxжсЁЂyжсНЛгкAЁЂBСНЕуЃЌ
ЁрAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌ2![]() ЃЉЃЌ
ЃЉЃЌ
ЁпХзЮяЯпyЃНЉ![]() +bx+cОЙ§AЁЂBСНЕуЃЌ
+bx+cОЙ§AЁЂBСНЕуЃЌ
ЁрНЋAЁЂBСНЕузјБъДњШыХзЮяЯпНтЮіЮіЕУЃК
Љ![]() Љ2b+cЃН0ЃЌcЃН2
Љ2b+cЃН0ЃЌcЃН2![]() ЃЌ
ЃЌ
ЁрbЃН![]() ЃЌcЃН2
ЃЌcЃН2![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЬтвтжЊA'ЃЈ2ЃЌ0ЃЉЃЌ
ЁрOA'ЃН2ЃЌ
ЁрtanЁЯA'BOЃН![]() ЃЌЫљвдЁЯOBA'ЃН30ЁуЃЌ
ЃЌЫљвдЁЯOBA'ЃН30ЁуЃЌ
ЁпLЮЊBFДЙжБЦНЗжЯпЩЯЕФЕуЃЌ
ЁрLBЃНLFЃНmЃЌ
ЁрЁЯLFBЃНЁЯLBFЃН30ЁуЃЌ
ЁрЁЯOLQЃН60ЁуЃЌBFЃН![]() mЃЌ
mЃЌ
ЁрOLЃНOBЉLBЃН2![]() ЉmЃЌ
ЉmЃЌ
ЩшLQЕФбгГЄЯпгыxжсНЛгкЕуDЃЌдђЁЯLDOЃН30ЁуЃЌ
ЁрODЃН![]() OLЃН6Љ
OLЃН6Љ![]() mЃЌ
mЃЌ
ЁпBF+ORЃН2ЃЌ
ЁрORЃН2ЉBFЃН2Љ![]() mЃЌ
mЃЌ
ЁрRDЃНODЉORЃН4ЃЌ
ЁпRQЁЭFLЃЌ
ЁрQRЃН![]() RDЃН2ЃЎ
RDЃН2ЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌЩшGЮЊABбгГЄЩЯвЛЕуЃЌзїBPЁЭABНЛxжсгкЕуPЃЌ
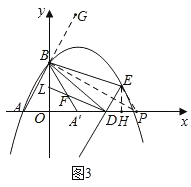
СЌНгEPЃЌзїEHЁЭxжсгкHЃЎ
ЁпtanЁЯBAOЃН![]() ЃЌ
ЃЌ
ЁрЁЯBAOЃН60ЁуЃЌ
ЁрЁЯBPAЃН30ЁуЃЌ
ЁпЁЯABE+ЁЯABDЃНЁЯABE+ЁЯGBEЃН180Ёу
ЁрЁЯABDЃНЁЯGBEЃЌ
ЁпBDЃНBEЃЌ
ЁрЁЯBDEЃНЁЯBEDЃЌ
ЁпЁЯABD+ЁЯDBE+ЁЯGBEЃНЁЯBDE+ЁЯDBE+ЁЯBEDЃН180ЁуЃЌ
ЁрЁЯABDЃНЁЯGBEЃНЁЯBDEЃНЁЯBEDЃЌ
ЁрABЁЮDEЃЌ
ЁрЁЯEDPЃНЁЯBAOЃН60ЁуЃЌ
ЁпBPЁЭABЃЌ
ЁрBPЁЭDEЃЌ
ЁрPEЃНPDЃЌ
ЁрЁїEDPЪЧЕШБпШ§НЧаЮЃЌ
ЁрPHЃНDHЃН![]() DPЃЌ
DPЃЌ
ЩшDЕузјБъЮЊЃЈnЃЌ0ЃЉЃЌ
ЁпOPЃН![]() OBЃН6ЃЌ
OBЃН6ЃЌ
ЁрPDЃНOPЉODЃН6ЉnЃЌ
ЁрDHЃНPHЃН![]()
ЁрEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
НЋEЕузјБъДњШыХзЮяЯпНтЮіЪННтЕУnЃН4ЛђnЃН![]() ЃЌ
ЃЌ
ЁрEЕузјБъЮЊ![]() Лђ
Лђ ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпx=tгыЗДБШР§КЏЪ§y=![]() ЃЌy=Љ
ЃЌy=Љ![]() ЕФЭМЯѓНЛгкЕуAЃЌBЃЌжБЯпy=2tгыЗДБШР§y=
ЕФЭМЯѓНЛгкЕуAЃЌBЃЌжБЯпy=2tгыЗДБШР§y=![]() ЃЌy=Љ
ЃЌy=Љ![]() ЕФЭМЯѓНЛгкЕуCЃЌDЃЌЦфжаГЃЪ§tЃЌkОљДѓгк0ЃЎЕуPЃЌQЗжБ№ЪЧxжсЁЂyжсЩЯШЮвтЕуЃЌШєSЁїPCD=S1ЃЌSЁїABQ=S2ЃЎдђЯТСаНсТле§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЕФЭМЯѓНЛгкЕуCЃЌDЃЌЦфжаГЃЪ§tЃЌkОљДѓгк0ЃЎЕуPЃЌQЗжБ№ЪЧxжсЁЂyжсЩЯШЮвтЕуЃЌШєSЁїPCD=S1ЃЌSЁїABQ=S2ЃЎдђЯТСаНсТле§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
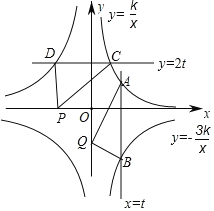
A.S1=2tB.S2=4kC.S1=2S2D.S1=S2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН8ЃЌBCЃН4ЃЌНЋОиаЮбиACелЕўЃЌЕуDТфдкЕуDЁфДІЃЌдђжиЕўВПЗжЁїAFCЕФУцЛ§ЮЊЃЈ ЃЉ

A.6B.8C.10D.12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧХзЮяЯпаЭЙАЧХЃЌЕБЙАЖЅРыЫЎУц2mЪБЃЌЫЎУцПэ4mЃЌЫЎУцЯТНЕ2mЃЌЫЎУцПэЖШдіМг______m.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯBACЃН30ЁуЃЌADЁЭBCгкDЃЌBDЃН4ЃЌCDЃН6ЃЌдђADЕФГЄЮЊ_____ЃЎ
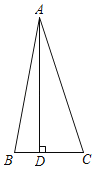
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊНјвЛВНЦеМАзуЧђжЊЪЖЃЌДЋВЅзуЧђЮФЛЏЃЌФГЪадкжааЁбЇОйааСЫЁАзуЧђдкЩэБпЁБжЊЪЖОКШќЛюЖЏЃЌИїРрЛёНБбЇЩњШЫЪ§ЕФБШР§ЧщПіШчЭМЫљЪОЃЌЦфжаЛёЕУШ§ЕШНБЕФбЇЩњЙВ50УћЃЌЧыНсКЯЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉЛёЕУвЛЕШНБЕФбЇЩњга ШЫЃЛ
ЃЈ2ЃЉдкБОДЮжЊЪЖОКШќЛюЖЏжаЃЌAЃЌBЃЌCЃЌD ЫФЫљбЇаЃБэЯжЭЛГіЃЌЯжОіЖЈДгетЫФЫљбЇаЃжаЫцЛњбЁШЁСНЫљбЇаЃОйаавЛГЁзуЧђгбвъШќЃЌЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓЧЁКУбЁЕНAЃЌBСНЫљбЇаЃЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦѓвЕдкМзЕигжвЛЙЄГЇЃЈМђГЦМзГЇЃЉЩњВњФГВњЦЗЃЌ2017ФъЕФФъВњСПЙ§АйЭђЃЌ2018ФъМзГЇОЙ§ММЪѕИФдьЃЌШеОљЩњВњЕФИУВњЦЗЪ§ЪЧИУГЇ2017ФъЕФ2БЖЛЙЖр2МўЃЎ
ЃЈ1ЃЉШєМзГЇ2018ФъЩњВњ200МўИУВњЦЗЫљашЕФЪБМфгы2017ФъЩњВњ98МўИУВњЦЗЫљашЕФЪБМфЯрЭЌЃЌдђ2017ФъМзГЇШеОљЩњВњИУВњЦЗЖрЩйМўЃП
ЃЈ2ЃЉгЩгкИУВњЦЗЩюЪмЙЫПЭЯВЛЖЃЌ2019ФъИУЦѓвЕдкввЕиНЈСЂаТГЇЃЈМђГЦввГЇЃЉЩњВњИУВњЦЗЃЌввГЇЕФШеОљЩњВњЕФИУВњЦЗЪ§ЪЧМзГЇ2017ФъЕФ3БЖЛЙвЊЖр5МўЃЌЭЌФъИУЦѓвЕвЊЧѓМзЁЂввСНГЇЗжБ№ЩњВњmЃЌnМўВњЦЗЃЈМзГЇЕФШеОљВњСПгы2018ФъЯрЭЌЃЉЃЌmЃКnЃН14ЃК25ЃЌШєМзЁЂввСНГЇЭЌЪБПЊЪМЩњВњЃЌЫЯШЭъГЩШЮЮёЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвдABЮЊжБОЖЕФЁбOОЙ§ACЕФжаЕуDЃЌDEЁЭBCгкЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКDEЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЕБABЃН4![]() ЃЌЁЯCЃН30ЁуЪБЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєИљКХКЭІаЃЉЃЎ
ЃЌЁЯCЃН30ЁуЪБЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєИљКХКЭІаЃЉЃЎ
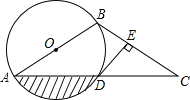
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌBDгыACЯрНЛгкEЕуЃЌAEЃНCEЃЌBCЃНACЃНDCЃЌдђtanЁЯABDtanЁЯADBЃН_____ЃЎ
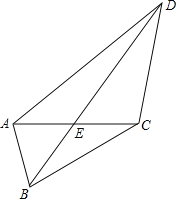
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com