
 如图,已知△ABC中,∠ACB=90°,CE是中线,△ACD与△ACE关于直线AC对称.
如图,已知△ABC中,∠ACB=90°,CE是中线,△ACD与△ACE关于直线AC对称.分析 (1)利用直线对称性得出△ACD≌△ACE,进而得出EA=EC=DA=DC,求出即可;
(2)利用平行四边形的判定得出四边形BCDE为平行四边形,进而得出答案.
解答 (1)证明:∵∠C=90°,点E为AB的中点,
∴EA=EC,
∵△ACD与△ACE关于直线AC对称.
∴△ACD≌△ACE,
∴EA=EC=DA=DC,
∴四边形ADCE是菱形;
(2)证明:∵四边形ADCE是菱形,
∴CD∥AE且CD=AE,
∵AE=EB,
∴CD∥EB且CD=EB
∴四边形BCDE为平行四边形,
∴DE=BC.
点评 此题主要考查了菱形的判定和证明线段相等的常用方法以及画图的规范和证明的严密性,正确把握菱形的判定是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
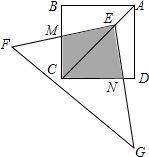 如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )
如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )| A. | $\frac{5}{9}$a2 | B. | $\frac{4}{9}$a2 | C. | $\frac{2}{3}$a2 | D. | $\frac{1}{4}$a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量y(件) | 500 | 490 | 480 | 470 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a0=1 | B. | 夹在两条平行线间的线段相等 | ||
| C. | 若$\frac{\sqrt{x-1}}{x-2}$有意义,则x≥1且x≠2 | D. | 勾股定理是a2+b2=c2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
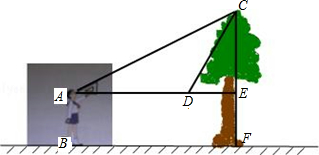 如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高AB为1.7m,求这棵树的高度.(结果精确到0.1m,$\sqrt{3}$≈1.73)
如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高AB为1.7m,求这棵树的高度.(结果精确到0.1m,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
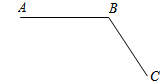 如图,平面上有A、B、C三点.
如图,平面上有A、B、C三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com