
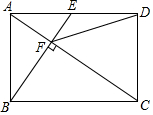
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①正确.只要证明∠EAC=∠ACB,∠ABC=∠AFE=90°即可;
②正确.由AD∥BC,推出△AEF∽△CBF,推出$\frac{AE}{BC}$=$\frac{AF}{CF}$,由AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,推出$\frac{AF}{CF}$=$\frac{1}{2}$,即CF=2AF;
③正确.只要证明DM垂直平分CF,即可证明;
④错误.设AE=a,AB=b,则AD=2a,由△BAE∽△ADC,有 $\frac{b}{a}$=$\frac{2a}{b}$,即b=$\sqrt{2}$a,可得tan∠CAD=$\frac{CD}{AD}$=$\frac{b}{2a}$=$\frac{\sqrt{2}}{2}$.
解答 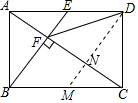 解:如图,过D作DM∥BE交AC于N,
解:如图,过D作DM∥BE交AC于N,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴$\frac{AE}{BC}$=$\frac{AF}{CF}$,
∵AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴$\frac{AF}{CF}$=$\frac{1}{2}$,
∴CF=2AF,故②正确;
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=$\frac{1}{2}$BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DM垂直平分CF,
∴DF=DC,故③正确;
设AE=a,AB=b,则AD=2a,
由△BAE∽△ADC,有 $\frac{b}{a}$=$\frac{2a}{b}$,即b=$\sqrt{2}$a,
∴tan∠CAD=$\frac{CD}{AD}$=$\frac{b}{2a}$=$\frac{\sqrt{2}}{2}$.故④错误;
故选B.
点评 本题主要考查了相似三角形的判定和性质,矩形的性质,图形面积的计算以及解直角三角形的综合应用,正确的作出辅助线构造平行四边形是解题的关键.解题时注意:相似三角形的对应边成比例.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:解答题
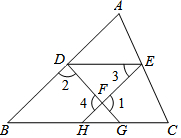 如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.
如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
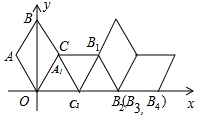 如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )
如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )| A. | (1343,0) | B. | (1347,0) | C. | (1343$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | D. | (1347$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com