
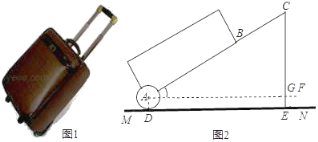
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A、B、C在同一条直线上,在箱体底端装有圆形的滚筒⊙A,⊙A与水平地面切于点D,在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平面的距离CE为59cm.设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为80cm,∠CAF=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:sin64°≈0.90,cos64°≈0.39,tan64°≈2.1)
【答案】(1)圆形滚轮的半径AD的长是8cm;(2)BC=30cm.
【解析】
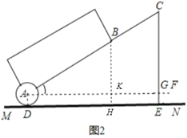
(1)作BH⊥AF于点K,交MN于点H,则△ABK∽△ACG,设圆形滚轮的半径AD的长是xcm,根据相似三角形的对应边的比相等,即可列方程求得x的值;
(2)求得CG的长,然后在直角△ACG中,求得AC即可解决问题;
(1)作BH⊥AF于点K,交MN于点H.
则BK∥CG,△ABK∽△ACG.
设圆形滚轮的半径AD的长是xcm.
则![]() ,即
,即![]() ,
,
解得:x=8.
则圆形滚轮的半径AD的长是8cm;
(2)在Rt△ACG中,CG=80﹣8=72(cm).
则sin∠CAF=![]() ,
,
∴AC=80,(cm)
∴BC=AC﹣AB=80﹣50=30(cm).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等的凸四边形叫做“准菱形”.利用该定义完成以下各题:
(1) 理解
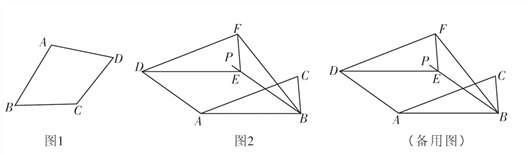
填空:如图1,在四边形ABCD中,若 (填一种情况),则四边形ABCD是“准菱形”;
(2)应用
证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)
(3) 拓展
如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,﹣1).
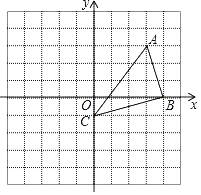
(1)以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A′B′C;
(2)在(1)中的条件下,
①点A经过的路径![]() 的长为 (结果保留π);②写出点B′的坐标为 .
的长为 (结果保留π);②写出点B′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
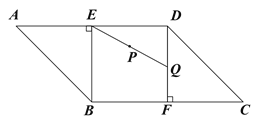
【题目】如图,已知平行四边形ABCD中,AD = 6,AB = ![]() ,∠A = 45°.过点B、D分别做BE⊥AD,DF⊥BC,交AD、BC与点E、F.点Q为DF边上一点,∠DEQ = 30°,点P为EQ的中点,过点P作直线分别与AD、BC相交于点M、N.若MN = EQ,则EM的长等于___________.
,∠A = 45°.过点B、D分别做BE⊥AD,DF⊥BC,交AD、BC与点E、F.点Q为DF边上一点,∠DEQ = 30°,点P为EQ的中点,过点P作直线分别与AD、BC相交于点M、N.若MN = EQ,则EM的长等于___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
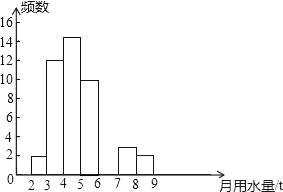
【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
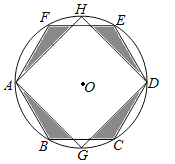
【题目】如图,在半径为6的⊙O中,正方形AGDH与正六边形ABCDEF都内接于⊙O,则图中阴影部分的面积为( )
A. 27﹣9![]() B. 54﹣18
B. 54﹣18![]() C. 18
C. 18![]() D. 54
D. 54
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果红旗商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
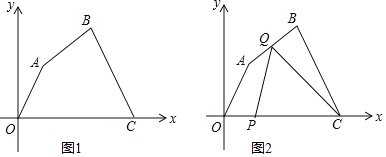
【题目】如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别为O(0,0),A(3,3![]() )、B(9,5
)、B(9,5![]() ),C(14,0),动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OA﹣AB﹣BC运动,在OA、AB、BC上运动的速度分别为3,
),C(14,0),动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OA﹣AB﹣BC运动,在OA、AB、BC上运动的速度分别为3,![]() ,
,![]() (单位长度/秒),当P、Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒),当P、Q中的一点到达C点时,两点同时停止运动.
(1)求AB所在直线的函数表达式;
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值;
(3)在P、Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com