
����Ŀ��ij�ֻ��������Ҹ������Ʒ���г��ϵ����������������ԭ����ÿ��2000Ԫ���۵�һ������ֻ����е��ۣ������µ��۵İ����Żݳ��ۣ����ÿ���ֻ��Կɻ��ʵ�����ۼ۵�20%����������=���ۼ����ɱ��ۣ�.��֪�ÿ��ֻ�ÿ���ɱ�����ԭ���۵��۵�60%.
��1����������������ֻ����µ�����ÿ������Ԫ���������ʵ�����ۼ���ÿ������Ԫ��
��2��Ϊʹ���갴�µ����������۵�������20��Ԫ����������Ӧ�����������ֻ����ٲ���
���𰸡���1���µ���Ϊÿ��1875Ԫ���������ʵ�����ۼ�ÿ��Ϊ1500Ԫ�� ��2����������Ӧ�����������ֻ�667��������ʹ���µ����������۵�������20��Ԫ.
��������
��1�����������֪����ĵ�����ϵ�У��ɱ���=60%ԭ���ۼ�=60%��2000���µ�����80%-�ɱ���=20%��ʵ���ۼۣ�ʵ�����ۼ�=�µ�����80%���������ϵ����������г����̣�
��2�����갴�µ����������۵�����=���������ܶ�-�ܳɱ��ۣ����������ܶ�=�����ֻ���������ʵ�����ۼۣ�
��1��������֪�ɱ���Ϊ��![]() %=1200��Ԫ��.
%=1200��Ԫ��.
���������ֻ����µ���Ϊÿ��![]() Ԫ.�������⣬��
Ԫ.�������⣬��
1200+20%80%![]() =80%
=80%![]() ��
��
��� ![]() . ���µ���Ϊÿ��1875Ԫ
. ���µ���Ϊÿ��1875Ԫ
���ԣ��������ʵ�����ۼ�ÿ��Ϊ��1875![]() 80%=1500��Ԫ��.
80%=1500��Ԫ��.
��2�������⣬�� ![]() ��200000��
��200000��
��� ![]() ��
��![]() .
.
��ˣ���������Ӧ�����������ֻ�667��������ʹ���µ����������۵�������20��Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����գ���1������x+![]() �ĸ���10������һ������_____��
�ĸ���10������һ������_____��
��2���������![]() �е�ֵ��ŵĸ�����ôm��_____��
�е�ֵ��ŵĸ�����ôm��_____��
��3���������x�ķ���![]() ��������x��1����k��_____��
��������x��1����k��_____��
��4������![]() �ĸ���_____��
�ĸ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
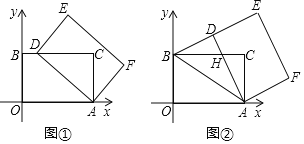
����Ŀ����ƽ��ֱ������ϵ�У��ı���AOBC�Ǿ��Σ���O��0��0������A��5��0������B��0��3�����Ե�AΪ���ģ�˳ʱ����ת����AOBC���õ�����ADEF����O��B��C�Ķ�Ӧ��ֱ�ΪD��E��F��
��1����ͼ�٣�����D����BC����ʱ�����D�����ꣻ
��2����ͼ�ڣ�����D�����߶�BE��ʱ��AD��BC���ڵ�H��
����֤��ADB�ա�AOB��
�����H�����꣮
��3����KΪ����AOBC�Խ��ߵĽ��㣬SΪ��KDE���������S��ȡֵ��Χ��ֱ��д��������ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��2�ֱ���ij������ܵ�ʵ��ͼ��ʾ��ͼ����֪����BC=0.60�ף�����BC��֧��AC���ɵĽ���ACB=75�㣬֧��AF�ij�Ϊ2.50�ף����嶥��F�㵽����D�ľ���FD=1.35�ף�����ײ�֧��HE��֧��AF���ɵĽ���FHE=60�㣬������D������ľ��루��ȷ��0.01�ף����ο����ݣ�cos75����0.2588��sin75����0.9659��tan75����3.732��![]() ��1.732��
��1.732��![]() ��1.414��
��1.414��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�������ij��ѧ���꼶ѧ��������ˮƽ�����г�鲿��ѧ���������������������ͼͳ��ͼ��
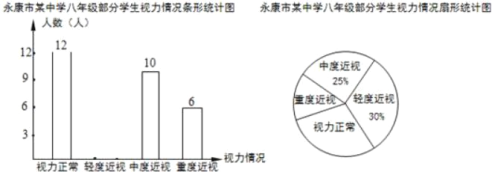
��1������������������ ��
��2���벹ȫ����ͳ��ͼ����������ͳ��ͼ����������������Բ�ĽǶ�����
��3����У���꼶����200λѧ��������Ƹ�У���꼶����������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
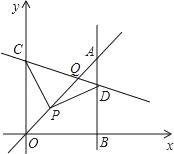
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���֪P��1��1����CΪy����������һ�㣬DΪ��һ������һ�㣬��PC��PD����CPD��90��������D��ֱ��AB��x����B��ֱ��AB��ֱ��y��x���ڵ�A����BD��3AD������CD��ֱ��CD��ֱ��y��x���ڵ�Q�����Q������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=![]() ��x��0����ͼ����3����1������1<y<3ʱ���Ա���x��ȡֵ��Χ��______��
��x��0����ͼ����3����1������1<y<3ʱ���Ա���x��ȡֵ��Χ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ�麬30����60����90����ֱ�����ǰ壬ֱ�Ƕ���Oλ������ԭ�㣬б��AB��ֱx�ᣬ����A�ں���y1��![]() ��x��0����ͼ���ϣ�����B�ں���y2��
��x��0����ͼ���ϣ�����B�ں���y2��![]() ��x��0����ͼ���ϣ���ABO��30������
��x��0����ͼ���ϣ���ABO��30������![]() ���� ��
���� ��

A. ��![]() B. ��
B. ��![]() C. ��
C. ��![]() D. ��
D. ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ���ԲO����BOC=120����ADΪԲO��ֱ����AD��BC��P����PB=1��PC=2����AC�ij�Ϊ( )
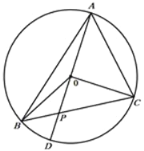
A. ![]() B.
B. ![]() C. 3D. 2
C. 3D. 2![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com