
【题目】如图,在△ABC中,AB=AC=4,∠BAC=120°,AD为BC边上的高,点P从点B以每秒![]() 个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
(1)求BC的长;
(2)设△PDQ的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围;
(3)在动点P、Q的运动过程中,是否存在PD=PQ,若存在,求出△PDQ的周长,若不存在,请说明理由.

【答案】(1) 4![]() ;(2)①S△PDQ=-
;(2)①S△PDQ=-![]() t2+
t2+![]() t(0≤t≤2);②S△PDQ=
t(0≤t≤2);②S△PDQ=![]() t -
t -![]() t2 (2<t≤4);(3)存在PD=PQ,此时△PDQ的周长为3
t2 (2<t≤4);(3)存在PD=PQ,此时△PDQ的周长为3![]() .
.
【解析】
(1)根据等腰三角形性质三线合一和含30°锐角的直角三角形的性质即可解答;(2)分当点P在线段BD上运动和当点P在线段DC上运动,过点Q作QM⊥BC于点M,用含时间t的代数式分别表示出PD=BD-BP=2![]() -
-![]() t或者PD= BP - BD =
t或者PD= BP - BD =![]() t- 2
t- 2![]() ,、QM
,、QM ![]() CQ=
CQ=![]() t的长,根据三角形面积公式即可求解;(3)根据题意可得,当PD=PQ时,PD=PQ,
t的长,根据三角形面积公式即可求解;(3)根据题意可得,当PD=PQ时,PD=PQ,
用含t的式子分别表示出Rt△PMQ的三边,由勾股定理得QM2+MP2=QP2,解得t=3后得到△DPQ是等边三角形,边长为![]() ,从而求出周长.
,从而求出周长.
解:(1)△ABC中,∵AB=AC=4,∠BAC=120°,AD⊥ BC,
∴∠B=∠C=30°,BD=DC
∴AD=![]() AB=2,由勾股定理得:BD=DC= 2
AB=2,由勾股定理得:BD=DC= 2![]()
∴BC=2BD=4![]() ;
;
(2)过点Q作QM⊥BC于点M,
∵CQ=t,∠C=30°,BP=![]() t
t
∴QM= ![]() CQ=
CQ=![]() t ,
t ,
①当点P在线段BD上运动时,即0≤t≤2,如图:
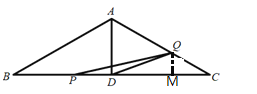
PD=BD-BP=2![]() -
-![]() t
t
∴S△PDQ=![]() ×PD×QM=
×PD×QM=![]() ×(2
×(2![]() -
-![]() t)×
t)×![]() t=-
t=-![]() t2+
t2+![]() t(0≤t≤2);
t(0≤t≤2);
②当点P在线段DC上运动时,即2<t≤4,如图:
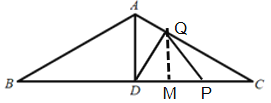
PD= BP - BD =![]() t- 2
t- 2![]() ,方法同①得:
,方法同①得:
S△PDQ=![]() ×PD×QM=
×PD×QM=![]() ×(
×(![]() t -2
t -2![]() )×
)×![]() t=
t=![]() t -
t -![]() t2 (2<t≤4);
t2 (2<t≤4);
(3)当点P在BD上运动时,∠BDQ>90°,PD≠PQ,所以若PD=PQ=![]() t -2
t -2![]() ,则PD=PQ如(2)②中图形,此时PD=PQ=
,则PD=PQ如(2)②中图形,此时PD=PQ=![]() t- 2
t- 2![]() ,PC=BC-BP=4
,PC=BC-BP=4![]() -
-![]() t,MC=
t,MC=![]() =
=![]() t ,MP=MC-PC=
t ,MP=MC-PC=![]() t-(4
t-(4![]() -
-![]() t)=
t)=![]() t-4
t-4![]() ,
,
Rt△PMQ中,∵QM2+MP2=QP2
∴(![]() t)2+(
t)2+(![]() t-4
t-4![]() )2=(
)2=(![]() t -2
t -2![]() )2,
)2,
化简得:t2-6t+9=0,即(t-3)2=9,∵t >0
解得t=3,即PD=PQ=![]() t -2
t -2![]() =3
=3![]() -2
-2![]() =
=![]() =PC,
=PC,
又∵∠C=30°,∴∠C=∠PQC=30°,∠DPQ=∠C+∠PQC=60°,即△DPQ是等边三角形,
∴△DPQ的周长=3PD=3![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排列,可以得到下面的等式(1),然后将每个式子的各项系数排列成(2):(a+b)1=a+b;(a+b)2=a2+2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a+b)4=a4+4a3b+6a2b2+4ab3+b4;根据规律可得:(a+b)5=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系:

解:CD⊥AB
∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠_____=90°(垂直定义)
∴DG∥AC,(____________________)
∴∠2=∠_________.(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠1=∠________(等量代换)
∴EF∥______(同位角相等,两直线平行)
∴∠AEF=∠ADC,(________________)
∵EF⊥AB,
∴∠AEF=90°
∴∠ADC=90°
即:CD⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A为平面直角坐标系第一象限内一点,直线y=x过点A,过点A作AD⊥y轴于点D,点B是y轴正半轴上一动点,连接AB,过点A作AC⊥AB交x轴于点C.
(1)如图,当点B在线段OD上时,求证:AB=AC;
(2)①如图,当点B在OD延长线上,且点C在x轴正半轴上, OA、OB、OC之间的数量关系为________(不用说明理由);
②当点B在OD延长线上,且点C在x轴负半轴上,写出OA、OB、OC之间的数量关系,并说明原因.
(3)直线BC分别与直线AD、直线y=x交于点E、F,若BE=5,CF=12,直接写出AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.

(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标
(3)求出△A1B1C1的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
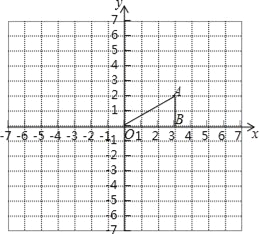
【题目】如图,点A的坐标为(3,2),点B的坐标为(3,0).作如下操作:
(1)以点A为旋转中心,将△ABO顺时针方向旋转90°,得到△AB1O1;
(2)以点O为位似中心,将△ABO放大,得到△A2B2O,使位似比为1:2,且点A2在第三象限.
①在图中画出△AB1O1和△A2B2O;
②请直接写出点A2的坐标: .
③如果△ABO内部一点M的坐标为(m,n),写出点M在△A2B2O内的对应点N的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A、B、C、D四组,如下表所示,同时,将调查结果绘制成下面两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:
(1)补全频数分布直方图和扇形统计图;
(2)所抽取的七年级学生早锻炼时间的中位数落在 区间内;
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
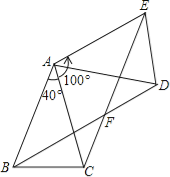
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com