
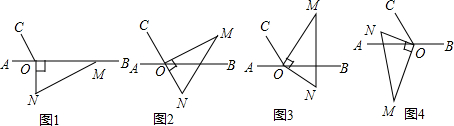
分析 (1)根据对顶角求出∠BON,代入∠BOM=∠MON-∠BON求出即可;
(2)求出∠BOC=120°,根据角平分线定义请求出∠COM=∠BOM=60°,代入∠CON=∠MON+∠COM求出即可;
(3)用∠AOM和∠CON表示出∠AON,然后列出方程整理即可得解.
解答 解:(1)如图2,∵∠AOC=60°,
∴∠BON=∠AOC=60°,
∵∠MON=90°,
∴∠BOM=∠MON-∠BON=30°,
故答案为:30°;
(2)∵∠AOC=60°,
∴∠BOC=180°-∠AOC=120°,
∵OM平分∠BOC,
∴∠COM=∠BOM=60°,
∵∠MON=90°,
∴∠CON=∠MON+∠COM=90°+60°=150°;
(3)∠AOM-∠NOC=30°,
理由是:∵∠MON=90°,∠AOC=60°,
∴∠AON=90°-∠AOM,
∠AON=60°-∠NOC,
∴90°-∠AOM=60°-∠NOC,
∴∠AOM-∠NOC=30°,
故∠AOM与∠NOC之间的数量关系为:∠AOM-∠NOC=30°.
点评 本题考查了旋转的性质,角平分线的定义,读懂题目信息并熟练掌握各性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
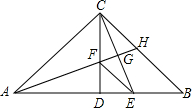 如图所示,在△ABC中,∠ACB=90°,CA=CB,CD⊥AB于点D,CE平分∠BCD,交AB于点E,AF平分∠CAD,交CD于点F.
如图所示,在△ABC中,∠ACB=90°,CA=CB,CD⊥AB于点D,CE平分∠BCD,交AB于点E,AF平分∠CAD,交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王老师获得一张2016宝应春节联欢晚会的门票,想奖给班级学校优秀的同学,通过考察,小明和小刚脱颖而出,但问题是只有一张门票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看晚会,他们各自提出了一个方案:
王老师获得一张2016宝应春节联欢晚会的门票,想奖给班级学校优秀的同学,通过考察,小明和小刚脱颖而出,但问题是只有一张门票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看晚会,他们各自提出了一个方案:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
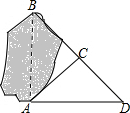 如图,为了测量出池塘两端A、B之间的距离,先在地面上取一点C,使∠ACB=90°,然后延长BD至D,使CD=BC,那么只要测量出AD的长度就得到A,B两点之间的距离,你能说明其中的道理吗?
如图,为了测量出池塘两端A、B之间的距离,先在地面上取一点C,使∠ACB=90°,然后延长BD至D,使CD=BC,那么只要测量出AD的长度就得到A,B两点之间的距离,你能说明其中的道理吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com