
 (4分)
(4分)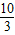 公顷蔬菜大棚.(5分)
公顷蔬菜大棚.(5分) )2+64 000(8分)
)2+64 000(8分) 时,75 000a-(27 000a+9000a2)的值最大为64 000元(9分)
时,75 000a-(27 000a+9000a2)的值最大为64 000元(9分) 公顷大棚,收益达到最大64 000元.(10分)
公顷大棚,收益达到最大64 000元.(10分)

 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.平均修建每公顷大棚要用的支架、塑料膜等材料的费用为27000元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为9000.每公顷大棚的年平均经济收益为75000元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后为60000元.
某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.平均修建每公顷大棚要用的支架、塑料膜等材料的费用为27000元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为9000.每公顷大棚的年平均经济收益为75000元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后为60000元.| 10 | 3 |
查看答案和解析>>
科目:初中数学 来源:2013年北师大版中考数学模拟试卷(八)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年湖北省武汉市中考数学模拟试卷(3)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com