
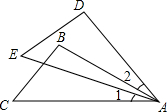
 如图,△ABC≌△ADE,∠1=30°,则∠2=30°.
如图,△ABC≌△ADE,∠1=30°,则∠2=30°. 分析 根据△ABC≌△ADE可以知道∠CAB=∠EAD,而∠EAB又是公共角,可以得到∠1=∠2,即可求得答案.
解答 解:∵△ABC≌△ADE,
∴∠CAB=∠EAD,
又∵∠CAB=∠1+∠EAB,∠EAD=∠2+∠EAB,
∴∠1+∠EAB=∠2+∠EAB,
∴∠1=∠2,
又∵∠1=30°,
∴∠2=30°,
故答案为:30°.
点评 本题主要考查了全等三角形的性质:全等三角形的对应角相等:①全等三角形的对应边上的高、中线以及对应角的平分线相等,②全等三角形的周长相等,面积相等,③平移、翻折、旋转前后的图形全等;关于全等三角形的性质应注意:①全等三角形的性质是证明线段和角相等的理论依据,应用时要会找对应角和对应边.②要正确区分对应边与对边,对应角与对角的概念,一般地:对应边、对应角是对两个三角形而言,而对边、对角是对同一个三角形的边和角而言的,对边是指角的对边,对角是指边的对角.解答本题的关键就是找到对应角,然后利用∠EAB是公共角进行求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com