
如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线 (k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是
(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是
A.1 B.2 C.3 D.4
B
解析试题分析:如图,作CE⊥y轴于点E,交双曲线于点G,作DF⊥x轴于点F, 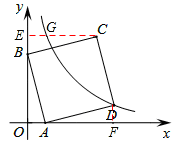
在y=﹣3x+3中,令x=0,解得:y=3,即B的坐标是(0,3)。
令y=0,解得:x=1,即A的坐标是(1,0)。
则OB=3,OA=1。
∵∠BAD=90°,∴∠BAO+∠DAF=90°。
又∵Rt△ABO中,∠BAO+∠OBA=90°,∴∠FAD=∠OBA。
∵在△OAB和△FDA中,∠OBA =∠FAD,∠AOB =∠DFA,AB=AD,
∴△OAB≌△FDA(AAS)。
同理,△OAB≌△FDA≌△BEC。
∴AF=OB=EC=3,DF=OA=BE=1。∴OF=OE=4。
∴D的坐标是(4,1),代入 得:k=4,则函数的解析式是:
得:k=4,则函数的解析式是: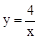 。
。
由OE=4得C的纵坐标是4,把y=4代入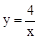 得:x=1,即G的坐标是(1,4)。
得:x=1,即G的坐标是(1,4)。
∴CG=2,即将正方形沿x轴负方向平移2个单位长度后,点C恰好落在该双曲线上。
∴a=2。故选B。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:单选题
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系: ,其图象为如图所示的一段曲线,且端点为
,其图象为如图所示的一段曲线,且端点为 和
和 ,若行驶速度不得超过60(km/h),则汽车通过该路段最少需要时间为( )
,若行驶速度不得超过60(km/h),则汽车通过该路段最少需要时间为( )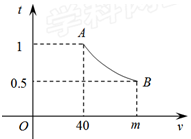
A. 分 分 | B.40分 | C.60分 | D. 分 分 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,直线 与双曲线
与双曲线 (k>0,x>0)交于点A,将直线
(k>0,x>0)交于点A,将直线 向上平移4个单位长度后,与y轴交于点C,与双曲线
向上平移4个单位长度后,与y轴交于点C,与双曲线 (k>0,x>0)交于点B,若OA=3BC,则k的值为
(k>0,x>0)交于点B,若OA=3BC,则k的值为
| A.3 | B.6 | C. | D. |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
(2013年四川自贡4分)如图,已知A、B是反比例函数 上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是【 】
上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是【 】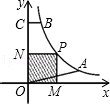
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com