
分析 (1)利用配方法把二次函数解析式配成顶点式得到抛物线的顶点坐标为[-(a+1),-a+2],利用坐标特征可确定直线l的解析式;
(2)如图1,设平移后的抛物线解析式为y=-(x-t)2+t+3,先通过解方程组$\left\{\begin{array}{l}{y=x+3}\\{y=-(x-t)^{2}+t+3}\end{array}\right.$得N(t-1,t+2),则可计算出MN=$\sqrt{2}$,所以EF=4,再解方程-(x-t)2+t+3=0得x1=t+$\sqrt{t+3}$,x2=t-$\sqrt{t+3}$,则EF=2$\sqrt{t+3}$,所以2$\sqrt{t+3}$=4,然后求出t即可得到平移后的抛物线解析式;
(3)如图2,作PH⊥x轴于H,先证明PA=PD得AH=DH,再确定A(-$\sqrt{c}$,0),C(0,c),设P(m,-m2+c),m>0,则D(2m+$\sqrt{c}$,0),利用待定系数法表示出直线CD的解析式为y=-mx+c,把D(2m+$\sqrt{c}$,0)代入得-m(2m+$\sqrt{c}$)+c=0,则$\sqrt{c}$=2m或$\sqrt{c}$=-m(舍去),接着利用三角形面积公式,利用S△ACP=S△ACD-S△APD得到$\frac{1}{2}$(2m+2$\sqrt{c}$)[c-(-m2+c)]=3,然后把$\sqrt{c}$=2m代入可求出m的值,从而得到c的值.
解答 解:(1)∵y=-x2-2ax-2x-a2-3a+1=-[x+(a+1)]2-a+2,
∴抛物线的顶点坐标为[-(a+1),-a+2],
而-a+2=-(a+1)+3,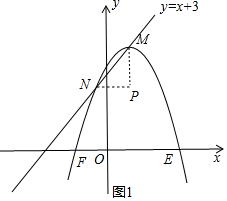
∴顶点在y=x+3上,
即直线l的解析式为y=x+3;
(2)当a=1时,抛物线解析式为y=-(x+2)2+1,
如图1,设平移后的抛物线解析式为y=-(x-t)2+t+3,
解方程组$\left\{\begin{array}{l}{y=x+3}\\{y=-(x-t)^{2}+t+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=t}\\{y=t+3}\end{array}\right.$或$\left\{\begin{array}{l}{x=t-1}\\{y=t+2}\end{array}\right.$,
则N(t-1,t+2),
∴MN=$\sqrt{(t-t+1)^{2}+(t+3-t-2)^{2}}$=$\sqrt{2}$,
∵EF=2$\sqrt{2}$MN,
∴EF=2$\sqrt{2}$×$\sqrt{2}$=4,
设E(x1,0),F(x2,0),
解方程-(x-t)2+t+3=0得x1=t+$\sqrt{t+3}$,x2=t-$\sqrt{t+3}$,
∴EF=t+$\sqrt{t+3}$-t+$\sqrt{t+3}$=2$\sqrt{t+3}$,
∴2$\sqrt{t+3}$=4,解得t=-1,
∴平移后的抛物线解析式为y=-(x+1)2+2;
(3)如图2,作PH⊥x轴于H,
∵∠APC=2∠PAB,
而∠APC=∠PAB+∠PDA,
∴∠PAD=∠PDA,
∴PA=PD,
∴AH=DH,
当y=0时,-x2+c=0,解得x1=$\sqrt{c}$,x2=-$\sqrt{c}$,则A(-$\sqrt{c}$,0),
当x=0时,y=-x2+c,则C(0,c),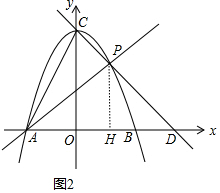
设P(m,-m2+c),m>0,则D(2m+$\sqrt{c}$,0),
设直线CD的解析式为y=kx+c,把P(m,-m2+c)代入得-m2+c=mk+c,解得k=-m,
∴直线CD的解析式为y=-mx+c,
把D(2m+$\sqrt{c}$,0)代入得-m(2m+$\sqrt{c}$)+c=0,
整理得c-m$\sqrt{c}$-2m2=0,解得$\sqrt{c}$=2m或$\sqrt{c}$=-m(舍去),
∵S△ACP=S△ACD-S△APD,
∴$\frac{1}{2}$(2m+2$\sqrt{c}$)[c-(-m2+c)]=3,
整理得(m+$\sqrt{c}$)•m2=3,
∴(m+2m)•m2=3,
解得m=1,
∴$\sqrt{c}$=2m=2,
∴c=4.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰三角形的性质;会利用待定系数法求一次函数和二次函数的解析式;会通过解方程组求二次函数与一次函数的交点坐标;理解坐标与图形性质.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
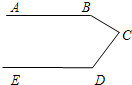 如图,一环湖公路的AB段为东西方向,经过三次拐弯后,又变成了东西方向的ED段,则∠B+∠C+∠D的度数为( )
如图,一环湖公路的AB段为东西方向,经过三次拐弯后,又变成了东西方向的ED段,则∠B+∠C+∠D的度数为( )| A. | 180° | B. | 270° | C. | 360° | D. | 450° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
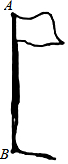 数学活动课上,老师组织学生测量学校旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面还多1米,当同学们把绳子的下端拉开5米后,发现绳子下端刚好接触地面,请你根据题意画出图形,并求旗杆的高度.
数学活动课上,老师组织学生测量学校旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面还多1米,当同学们把绳子的下端拉开5米后,发现绳子下端刚好接触地面,请你根据题意画出图形,并求旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
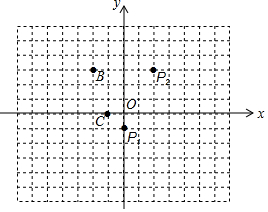 阅读理解:我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).
阅读理解:我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
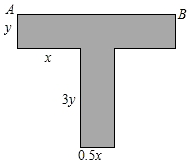 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com