
【题目】如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是_____.
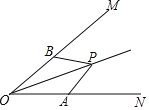
【答案】AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).
【解析】
根据题意已知∠AOP=∠BOP,再根据全等三角形的判定定理补充条件即可.
解:可以添加的条件有:AO=BO,∠OAP=∠OBP,∠APO=∠BPO,
证明:∵OP为∠MON的平分线,
∴∠AOP=∠BOP,
若添加的条件为AO=BO,
在△AOP和△BOP中,
OA=OB,∠AOP=∠BOP,OP=OP,
∴△AOP≌△BOP.
所以添加的条件为AO=BO,能得到△AOP≌△BOP;
若添加的条件为∠OAP=∠OBP,
在△AOP和△BOP中,
∠OAP=∠OBP,∠AOP=∠BOP,OP=OP,
∴△AOP≌△BOP.
所以添加的条件为∠OAP=∠OBP,能得到△AOP≌△BOP;
若添加的条件为∠APO=∠BPO,
在△AOP和△BOP中,
∠AOP=∠BOP,OP=OP,∠APO=∠BPO
∴△AOP≌△BOP.
所以添加的条件为∠APO=∠BPO,能得到△AOP≌△BOP;
故答案为AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 30 | 42 |
租金/(元/辆) | 300 | 400 |
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与探究:
如图,已知点A、O、B是正方形网格的格点(网格线的交点),点P是∠AOB的边0B上的一点.
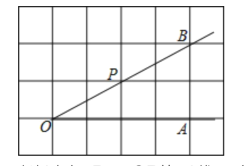
(1)过点P画OB的垂线,交OA于点E;
(2)过点P画OA的垂线,垂足为H;
(3)过点P画OA的平行线PC;
(4)若每个小正方形的边长是1,则点P到OA的距离是_________;
(5)线段PE、PH、OE的大小关系是___________(用“<"连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛,成绩如图所示:
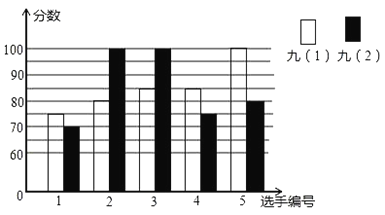
(1)根据图示填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | ||
九(2) | 85 | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的证明过程,指出其错误.(在错误部分下方划线)已知△ABC,求证:∠A+∠B+∠C=180°
(1)证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(作图)
∴∠2=∠B(内错角相等两直线平行)
∵∠1=∠C(作图)
∴∠B+∠C+∠3=∠2+∠1+∠3(等量代换)
∠2+∠l+∠3=180°(周角的定义)
即∠BAC+∠B+∠C=180°(等量代换)
(2)类比探究:请同学们参考图2,模仿(1)的解决过程,避免(1)中的错误,试说明求证:∠A+∠B+∠C=180°
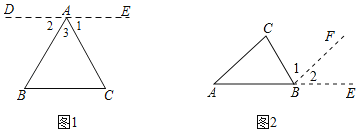
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AB=AD. ∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.

图1 图2 图3
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合.由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线. 易证△AFG![]() ,故EF,BE,DF之间的数量关系为 ;
,故EF,BE,DF之间的数量关系为 ;
(2)类比引申
如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°. 若BD=1,EC=2,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】购买甲、乙、丙三种不同品种的练习本各四次,其中,有一次购买时,三种练习本同时打折,四次购买的数量和费用如下表:
购买次数 | 购买各种练习本的数量(单位:本) | 购买总费用(单位:元) | ||
甲 | 乙 | 丙 | ||
第一次 | 2 | 3 | 0 | 24 |
第二次 | 4 | 9 | 6 | 75 |
第三次 | 10 | 3 | 0 | 72 |
第四次 | 10 | 10 | 4 | 88 |
(1)第______次购物时打折;练习本甲的标价是_____元/本,练习本乙的标价是______元/本,练习本丙的标价是______元/本;
(2)如果三种练习本的折扣相同,请问折扣是打几折?
(3)现有资金100.5元,全部用于购买练习本,计划以标价购进练习本36本,如果购买其中两种练习本,请你直接写出一种购买方案,不需说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,![]() ,
,![]() ,垂足分别为D、F,
,垂足分别为D、F,![]() ,请试说明
,请试说明![]() .
.
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (____________________________)
(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
又∵![]() (已知)
(已知)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com