
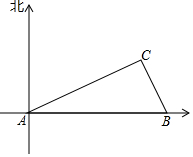
 如图,在我国沿海有一艘不明国国籍的轮船进入我国海域.我海军甲、乙两艘巡逻艇立即从相距13n mile的A、B两个基地前去拦截,18min后同时到达C地将其拦截.已知甲巡逻艇每小时航行40n mile,乙巡逻艇每小时航行18$\frac{2}{3}$n mile且航向为北偏西23°,求甲巡逻艇的航向.
如图,在我国沿海有一艘不明国国籍的轮船进入我国海域.我海军甲、乙两艘巡逻艇立即从相距13n mile的A、B两个基地前去拦截,18min后同时到达C地将其拦截.已知甲巡逻艇每小时航行40n mile,乙巡逻艇每小时航行18$\frac{2}{3}$n mile且航向为北偏西23°,求甲巡逻艇的航向. 分析 根据题意可以求得AC和BC的长,然后根据三角函数可以求得∠ACD的度数,从而可以求得甲巡逻艇的航向.
解答  解:由题意可得,
解:由题意可得,
AC=40×$\frac{18}{60}$=12,BC=$18\frac{2}{3}×\frac{18}{60}$=5.6,
作CD⊥AB于点D,如右图所示,
∵∠BCD=23°,cos∠BCD=$\frac{CD}{BC}$,cos∠ACD=$\frac{CD}{AC}$,
∴CD=BC•cos∠BCD,CD=AC•cos∠ACD,
∴5.6•cos23°=12•cos∠ACD,
解得,∠ACD≈65°,
即甲巡逻艇的航向是北偏东65°.
点评 本题考查解直角三角形的应用-方向角问题,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数解答.


科目:初中数学 来源: 题型:选择题
 如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )| A. | 俯视图与主视图相同 | B. | 左视图与主视图相同 | ||
| C. | 左视图与俯视图相同 | D. | 三个视图都相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
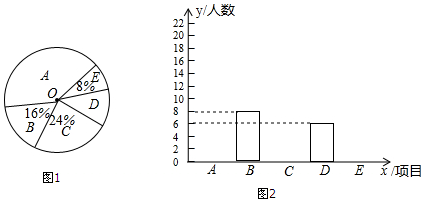
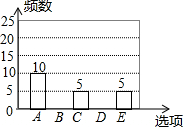 随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到图表(部分信息未给出):
随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到图表(部分信息未给出):| 选项 | 频数 | 频率 |
| A | 10 | m |
| B | n | 0.2 |
| C | 5 | 0.1 |
| D | p | 0.4 |
| E | 5 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,甲、乙两艘军舰分别在海面上的A、B处训练,且A、B两处相距50海里,甲、乙两艘军舰接到命令沿直线前往基地C,甲军舰以15海里/小时的速度前往,同时乙军舰以20海里/小时的速度前往,两小时后甲、乙两艘军舰间时到达基地C.已知基地C在A的北偏东37°方向,B在A的正东方向.
如图,甲、乙两艘军舰分别在海面上的A、B处训练,且A、B两处相距50海里,甲、乙两艘军舰接到命令沿直线前往基地C,甲军舰以15海里/小时的速度前往,同时乙军舰以20海里/小时的速度前往,两小时后甲、乙两艘军舰间时到达基地C.已知基地C在A的北偏东37°方向,B在A的正东方向.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
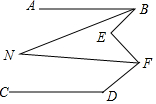 如图所示,AB∥CD,BN、FN分别平分∠ABE、∠EFD.已知∠BNF=α,∠BEF=β,∠FDC=γ,则下列等式中成立的是( )
如图所示,AB∥CD,BN、FN分别平分∠ABE、∠EFD.已知∠BNF=α,∠BEF=β,∠FDC=γ,则下列等式中成立的是( )| A. | α+β+γ=180° | B. | -2α+β+γ=180° | C. | α+β+γ=360° | D. | -2α+β+γ=360° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
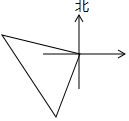 某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西70°方向航行50千米,第二艘快艇沿南偏西20°方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是( )
某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西70°方向航行50千米,第二艘快艇沿南偏西20°方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是( )| A. | 南偏东25°,50$\sqrt{2}$千米 | B. | 北偏西25°,50$\sqrt{2}$千米 | ||
| C. | 南偏东70°,100千米 | D. | 北偏西20°,100千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com