
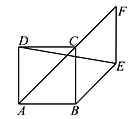
【题目】如图,四边形ABCD是正方形,AB=1,点F是对角线AC延长线上一点,以BC、CF为邻边作菱形BEFC,连接DE,则DE的长是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
【答案】C
【解析】
延长DC交EF于G,则CG⊥EF,由正方形和菱形的性质得出∠FCG=∠ACD=45°,CD=BC=CF=EF=1,得出△CFG是等腰直角三角形,得出CG=FG![]() ,求出DG=CD+CG=1
,求出DG=CD+CG=1![]() ,GE=EF﹣FG=1
,GE=EF﹣FG=1![]() .在Rt△DEG中,由勾股定理即可得出答案.
.在Rt△DEG中,由勾股定理即可得出答案.
延长DC交EF于G,如图所示,则CG⊥EF,∴∠CGF=∠CGE=90°.
∵四边形ABCD是正方形,四边形BEFC是菱形,∴∠FCG=∠ACD=45°,CD=BC=CF=EF=1,∴△CFG是等腰直角三角形,∴CG=FG![]() CF
CF![]() ,∴DG=CD+CG=1
,∴DG=CD+CG=1![]() ,GE=EF﹣FG=1
,GE=EF﹣FG=1![]() .在Rt△DEG中,由勾股定理得:DE
.在Rt△DEG中,由勾股定理得:DE![]() .
.
故选C.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】.中学生带手机上学的现象越来越受到社会的关注,为此某记者随机调查了某市城区若干名中学生家长对这种现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)根据抽样调查结果,请你估计该市城区6000名中学生家长中有多少名家长持反对态度.
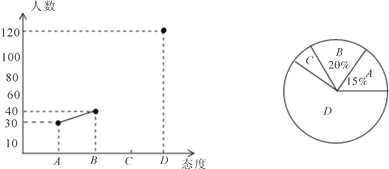
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)和点B,化简![]() 的结果为: ①c;②;③b﹣a;④a﹣b+2c.其中正确的有( )
的结果为: ①c;②;③b﹣a;④a﹣b+2c.其中正确的有( )
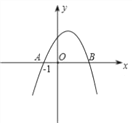
A. 一个 B. 两个 C. 三个 D. 四个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有4个小球,分别标有1,2,3,7四个数字,这些小球除所标数字不同外,其余方面完全相同,甲、乙两人每次同时从袋子中各随机摸出一个小球,记下小球上的数字,并计算它们的和.
(1)请用画树状图或列表的方法,求两数和是8的概率;
(2)甲、乙两人想用这种方法做游戏,他们规定:若两数之和是2的倍数时,甲得3分;若两数之和是3的倍数时,乙得2分;当两数之和是其他数值时,两人均不得分.你认为这个游戏公平吗?请说明理由;若你认为不公平,请你修改得分规则,使游戏公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”![]() 是近时期网络流行语,像一个人脸郁闷的神情
是近时期网络流行语,像一个人脸郁闷的神情![]() 如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案
如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案![]() 阴影部分
阴影部分![]() 设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
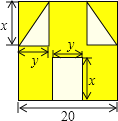
(1)用含有x、y的代数式表示下图中“囧”的面积;
(2)当![]() ,
,![]() 时,求此时“囧”的面积.
时,求此时“囧”的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水质量的需求越来越高,我市某公司根据市场需求准备销售A、B两种型号的净水器,每台A型净水器比每台B型净水器进价多300元,用48000元购进A型净水器与用36000元购进B型净水器的数量相等.
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A、B两种型号的净水器共400台进行销售,其中A型的台数不超过B型的台数,A型净水器每台售价1500元,B型净水器每台售价1100元,怎样安排进货才能使售完这400台净水器所获利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
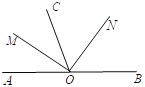
【题目】如图,O为直线AB上一点,OM是∠AOC的角平分线,ON是∠COB的平分线
(1)指出图中所有互为补角的角,
(2)求∠MON的度数,
(3)指出图中所有互为余角的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com