
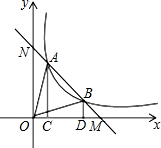
 如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{2}{x}$交于点A(1,2),与x轴交于点M,与y轴交于点N.
如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{2}{x}$交于点A(1,2),与x轴交于点M,与y轴交于点N.分析 (1)把M,A代入一次函数解析式,即可求得解析式,让一次函数解析式和反比例函数解析式组成方程组可求得另一交点坐标;
(2)看是否有等底等高的三角形,以及由面积相同的三角形减去同一三角形得到的四边形.
解答 解:(1)∵一次函数y=kx+b(k≠0)的图象经过A(1,2),M(3,0),
∴$\left\{\begin{array}{l}{k+b=2}\\{3k+b=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴一次函数解析式为y=-x+3;
解$\left\{\begin{array}{l}{y=-x+3}\\{y=\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=1}\end{array}\right.$,
∴B点的坐标为(2,1);
(2)解:∵k=2,
∴S△AOC=A△BOD=$\frac{|k|}{2}$=1,
∴都减去S△COE,
∴梯形BECD的面积与△AOE面积相等,
由三角形中位线知E为OB中点,
∴△ABE的面积与△AOE面积相等,
∴与△AOE面积相等的图形有△ABE、梯形BECD.
点评 本题考查了反比例函数和一次函数的交点问题,待定系数法求一次函数的解析式,三角形的面积和四边形的面积等.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:选择题
 三个微生物(分别标号为1,2,3)第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物.那么标号为100的微生物会出现在( )
三个微生物(分别标号为1,2,3)第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物.那么标号为100的微生物会出现在( )| A. | 第3天 | B. | 第4天 | C. | 第5天 | D. | 第6天 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面积为2000平方米的长方形临时仓库,并在其中一边上留宽为3米的大门,求无门的那边长.
如图,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面积为2000平方米的长方形临时仓库,并在其中一边上留宽为3米的大门,求无门的那边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com