
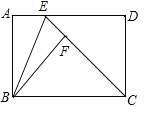
【题目】如图,矩形ABCD中,BC>AB,E是AD上一点,△ABE沿BE折叠,点A恰好落在线段CE的点F处,连结BF.
(1)求证:BC=CE;
(2)设![]() =k.
=k.
①若k=![]() ,求sin∠DCE的值;
,求sin∠DCE的值;
②设![]() =m,试求m与k满足的关系式.
=m,试求m与k满足的关系式.
【答案】(1)证明见解析;(2)①![]() ;②m2=2k﹣k2..
;②m2=2k﹣k2..
【解析】
(1)根据折叠的性质得到∠BEA=∠BEF,根据平行线的性质、等腰三角形的判定定理证明;
(2)①根据矩形的性质、正弦的定义计算;
②根据题意用AD表示出AB、AD,根据勾股定理列式计算即可.
(1)证明:由折叠的性质可知,∠BEA=∠BEF,
∵AD∥BC,
∴∠BEA=∠EBC,
∴∠BEF=∠EBC,
∴BC=CE;
(2)解:①∵![]() =
=![]() ,
,
∴AD=5AE,
∴DE=4AE,
∵BC=CE,
∴CE=5AE,
∴sin∠DCE=![]() =
=![]() ;
;
②∵![]() =k,
=k,![]() =m,
=m,
∴AE=kAD,AB=mAD,
∴DE=AD﹣AE=AD(1﹣k),
在Rt△CED中,CE2=CD2+DE2,即AD2=(mAD)2+[AD(1﹣k)]2,
整理得,m2=2k﹣k2.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为![]() 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
操作与发现:
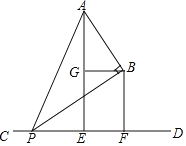
如图,已知A,B两点在直线CD的同一侧,线段AE,BF均是直线CD的垂线段,且BF在AE的右边,AE=2BF,将BF沿直线CD向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线CD相交于点P,点G是AE的中点,连接BG.
探索与证明:求证:
(1)四边形EFBG是矩形;
(2)△ABG∽△PBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,边CD的中垂线交对角线BD于点E,交CD于点F,连结AE.若∠ABC=50°,则∠AEB的度数为( )
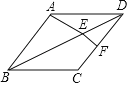
A.30°B.40°C.50°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB<BC.
(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则DE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
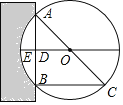
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师布置了一个作业,如下:已知:如图1![]() 的对角线
的对角线![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.
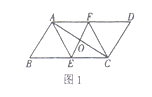

某同学写出了如图2所示的证明过程,老师说该同学的作业是错误的.请你解答下列问题:
(1)能找出该同学错误的原因吗?请你指出来;
(2)请你给出本题的正确证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,如图记录了跑的最快的一位选手与最慢的一位选手的跑步过程(最快的选手跑完了全程),其中x表示最快的选手的跑步时间,y表示这两位选手之间的距离,现有以下4种说法,正确的有( )
①最快的选手到达终点时,最慢的选手还有15米未跑;
②跑的最快的选手用时4'46″;
③出发后最快的选手与最慢的选手相遇了两次;
④出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时长.
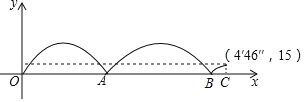
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com