
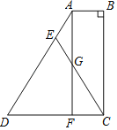
【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且AB=FC,E为AD上一点,EC交AF于点G,EA=EG.
求证:ED=EC.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
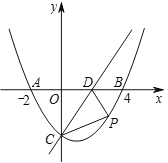
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的解析式.
(2)点![]() 是抛物线上第四象限上的一个动点,连接
是抛物线上第四象限上的一个动点,连接![]() ,
,![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
(3)将抛物线的对称轴向左平移3个长度单位得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若直线
,若直线![]() 上存在使
上存在使![]() 最大的点
最大的点![]() ,请直接写出满足条件的点
,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且点
两点,且点![]() ,点
,点![]() 在
在![]() 轴正半轴上运动,过点
轴正半轴上运动,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() .
.
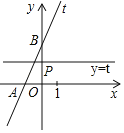
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)当![]() 时,直线
时,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)当![]() 时,若直线
时,若直线![]() 与直线
与直线![]() 和(2)反比例函数的图象分别交于点
和(2)反比例函数的图象分别交于点![]() ,
,![]() ,当
,当![]() 间距离大于等于2时,求
间距离大于等于2时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
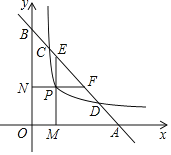
【题目】如图,直线y=﹣x+4分别交x轴、y轴于A、B两点,P是反比例函数y=![]() (x>0),图象上位于直线y=﹣x+4下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F,并且AFBE=4
(x>0),图象上位于直线y=﹣x+4下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F,并且AFBE=4
(1)求k的值;
(2)若反比例函数y=![]() 与一次函数y=﹣x+4交于C、D两点,求三角形OCD的面积.
与一次函数y=﹣x+4交于C、D两点,求三角形OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
由于发展时间早、发展速度快,经过20多年大规模的高速开发建设,北京四环内,甚至五环内可供开发建设的土地资源越来越稀缺,更多的土地供应将集中在五环外,甚至六环外的远郊区县.
据中国经济网2017年2月报道,来自某市场研究院的最新统计,2016年,剔除了保障房后,在北京新建商品住宅交易量整体上涨之时,北京各区域的新建商品住宅交易量则是有涨有跌![]() 其中,昌平、通州、海淀、朝阳、西城、东城六区下跌,跌幅最大的为朝阳区,新建商品住宅成交量比2015年下降了
其中,昌平、通州、海淀、朝阳、西城、东城六区下跌,跌幅最大的为朝阳区,新建商品住宅成交量比2015年下降了![]() 而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨,涨幅最大的为顺义区,比2015年上涨了
而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨,涨幅最大的为顺义区,比2015年上涨了![]() 另外,从环线成交量的占比数据上,同样可以看出成交日趋郊区化的趋势
另外,从环线成交量的占比数据上,同样可以看出成交日趋郊区化的趋势![]() 根据统计,2008年到2016年,北京全市成交的新建商品住宅中,二环以内的占比逐步从
根据统计,2008年到2016年,北京全市成交的新建商品住宅中,二环以内的占比逐步从![]() 下降到了
下降到了![]() ;二、三环之间的占比从
;二、三环之间的占比从![]() 下降到了
下降到了![]() ;三、四环之间的占比从
;三、四环之间的占比从![]() 下降到了
下降到了![]() ;四、五环之间的占比从
;四、五环之间的占比从![]() 下降到了
下降到了![]() 也就是说,整体成交中位于五环之内的新房占比,从2008年的
也就是说,整体成交中位于五环之内的新房占比,从2008年的![]() 下降到了2016年的
下降到了2016年的![]() ,下滑趋势非常明显
,下滑趋势非常明显![]() 由此可见,新房市场的远郊化是北京房地产市场发展的大势所趋
由此可见,新房市场的远郊化是北京房地产市场发展的大势所趋![]() 注:占比,指在总数中所占的比重,常用百分比表示
注:占比,指在总数中所占的比重,常用百分比表示![]()
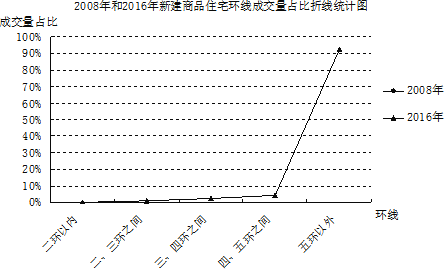
根据以上材料解答下列问题:
![]() 补全折线统计图;
补全折线统计图;
![]() 根据材料提供的信息,预估2017年位于北京市五环之内新建商品住宅成交量占比约______ ,你的预估理由是______ .
根据材料提供的信息,预估2017年位于北京市五环之内新建商品住宅成交量占比约______ ,你的预估理由是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
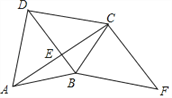
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2),若x1x2+y1y2=0,且A,B均不为原点,则称A和B互为正交点.比如:A(1,1),B(2,﹣2),其中1×2+1×(﹣2)=0,那么A和B互为正交点.
(1)点P和Q互为正交点,P的坐标为(﹣2,3),
①如果Q的坐标为(6,m),那么m的值为多少;
②如果Q的坐标为(x,y),求y与x之间的关系式;
(2)点M和N互为正交点,直接写出∠MON的度数;
(3)点C,D是以(0,2)为圆心,半径为2的圆上的正交点,以线段CD为边,构造正方形CDEF,圆心F在正方形CDEF的外部,求线段OE长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生体质,某校对学生设置了体操、球类、跑步、游泳等课外体育活动,为了了解学生对这些项目的喜爱情况,在全校范围内随机抽取了若干名学生,对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
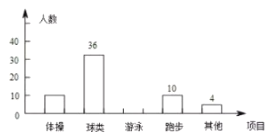
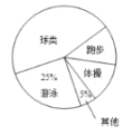
(1)在这次问卷调查中,一共抽查了多少名学生?
(2)补全频数分布直方图,求出扇形统计图中“体操”所对应的圆心角度数;
(3)估计该校![]() 名学生中有多少人喜爱跑步项目.
名学生中有多少人喜爱跑步项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数闭区间[m,n]上的“闭函数”.如函数y=﹣x+4.当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”
(1)反比例函数![]() 是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
(2)若二次函数y=x2﹣2x﹣k是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com