
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分图形的面积为$\frac{8π}{3}$.
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分图形的面积为$\frac{8π}{3}$. 分析 根据垂径定理求得CE=ED=2$\sqrt{3}$,然后由圆周角定理知∠COE=60°,然后通过解直角三角形求得线段OC、OE的长度,最后将相关线段的长度代入S阴影=S扇形OCB-S△COE+S△BED.
解答 解:如图,假设线段CD、AB交于点E,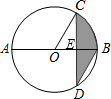
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=2$\sqrt{3}$,
又∵∠CDB=30°,
∴∠COE=2∠CDB=60°,∠OCE=30°,
∴OE=CE•cot60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,OC=2OE=4,
∴S阴影=S扇形OCB-S△COE+S△BED=$\frac{60π×O{C}^{2}}{360}$-$\frac{1}{2}$OE×EC+$\frac{1}{2}$BE•ED=$\frac{8π}{3}$-2$\sqrt{3}$+2$\sqrt{3}$=$\frac{8π}{3}$.
故答案为:$\frac{8}{3}π$.
点评 考查了垂径定理、扇形面积的计算,通过解直角三角形得到相关线段的长度是解答本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 121(1-x)2=100 | B. | 121(1+x)2=100 | C. | 100(1-x)2=121 | D. | 100(1+x)2=121 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | 10800 | 11000 | 11200 | 11400 | … |
| y | … | 30 | 25 | 20 | 15 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
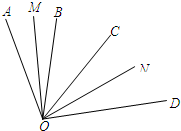 如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com