
分析 (1)去分母化分式方程为整式方程,解整式方程求得x的值,继而检验可得答案;
(2)公式法求解可得.
解答 解:(1)去分母,得:6=x+2x+2,
解得:x=$\frac{4}{3}$,
经检验x=$\frac{4}{3}$是原分式方程的解,
∴原方程的解为x=$\frac{4}{3}$;
(2)∵a=1,b=-3,c=-1,
∴△=9+4=13>0,
∴x=$\frac{3±\sqrt{13}}{2}$,
即x1=$\frac{3+\sqrt{13}}{2}$,x2=$\frac{3-\sqrt{13}}{2}$.
点评 本题主要考查解分式方程和一元二次方程的能力,熟练掌握解方程的基本依据和步骤是解题的关键.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
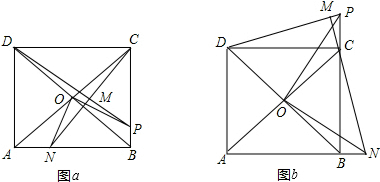
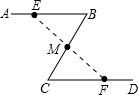 如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么?
如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
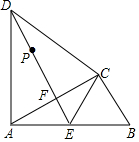 如图,在△ABC中,∠ACB=90°,以AC为底边作等腰三角形△ACD,AD=CD,E为AB的中点,连接CE、DE,DE与AC相交于点F.
如图,在△ABC中,∠ACB=90°,以AC为底边作等腰三角形△ACD,AD=CD,E为AB的中点,连接CE、DE,DE与AC相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
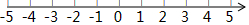 结合数轴与绝对值的知识回答下列问题:
结合数轴与绝对值的知识回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
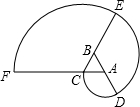 如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).
如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com