
【题目】如图,一次函数y1=kx+b(k≠0)和反比例函数![]() 的图象相交于点A(﹣4,2),B(n,﹣4)
的图象相交于点A(﹣4,2),B(n,﹣4)
(1)求一次函数和反比例函数的表达式;
(2)观察图象,直接写出不等式y1<y2的解集.

科目:初中数学 来源: 题型:
【题目】某商店老板准备购买A、B两种型号的足球共100只,已知A型号足球进价每只40元,B型号足球进价每只60元.
(1)若该店老板共花费了5200元,那么A、B型号足球各进了多少只;
(2)若B型号足球数量不少于A型号足球数量的![]() ,那么进多少只A型号足球,可以让该老板所用的进货款最少?
,那么进多少只A型号足球,可以让该老板所用的进货款最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,抛物线![]() 经过点A(5,0)、B(-3,4),抛物线的对称轴与x轴相交于点D.
经过点A(5,0)、B(-3,4),抛物线的对称轴与x轴相交于点D.
(1)求抛物线的表达式;
(2)联结OB、BD.求∠BDO的余切值;
(3)如果点P在线段BO的延长线上,且∠PAO =∠BAO,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油最多可行驶的公里数,如图描述了A、B两辆汽车在不同速度下的燃油效率情况.
根据图中信息,下面4个推断中,合理的是( )
①消耗1升汽油,A车最多可行驶5千米;
②B车以40千米/小时的速度行驶1小时,最多消耗4升汽油;
③对于A车而言,行驶速度越快越省油;
④某城市机动车最高限速80千米/小时,相同条件下,在该市驾驶B车比驾驶A车更省油.
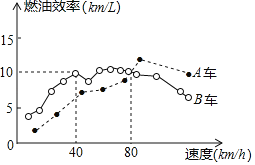
A.①④B.②③C.②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在A、B两个校区各有九年级学生200人,为了解这两个校区九年级学生的教学学业水平的情况,进行了抽样调查,过程如下,请补充完整.
收集数据:从A、B两个校区各随机抽取20名学生,进行了数学学业水平测试,测试成绩(百分制)如下:
A校区 86 74 78 81 76 75 86 70 75 90
75 79 81 70 74 80 87 69 83 77
B校区 80 73 70 82 71 82 83 93 77 80
81 93 81 73 88 79 81 70 40 83
整理、描述数据 按如下分数段整理、描述这两组样本数据:
成绩x 人数 校区 | 40≤x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
A | 0 | 0 | 1 | 11 | 7 | 1 |
B |
(说明:成绩80分及以上的学业水平优秀,70﹣79分为淡定业水平良好,60﹣69分为学业水平合格,60分以下为学业水平不合格)
分析数据 两组样本数据的平均数、中位数、众数如下表所示:
校区 | 平均数 | 中位数 | 众数 |
A | 78.3 | m | 75 |
B | 78 | 80.5 | 81 |
其中m= ;
得出结论:a.估计B校区九年级数学学业水平在优秀以上的学生人数为 ;
b.可以推断出 校区的九年级学生的数学学业水平较高,理由为 (至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,已知抛物线y=ax2﹣3x+c与y轴交于点A(0,﹣4),与x轴交于点B(4,0),点P是线段AB下方抛物线上的一个动点.
(1)求这条抛物线的表达式及其顶点的坐标;
(2)当点P移动到抛物线的什么位置时,∠PAB=90°求出此时点P的坐标;
(3)当点P从点A出发,沿线段AB下方的抛物线向终点B移动,在移动中,设点P的横坐标为t,△PAB的面积为S,求S关于t的函数表达式,并求t为何值时S有最大值,最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
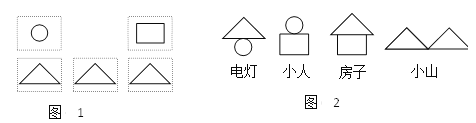
【题目】杨华与季红用5张同样规格的硬纸片做拼图游戏,正面如图1所示,背面完全一样,将它们背面朝上搅匀后,同时抽出两张.规则如下:当两张硬纸片上的图形可拼成电灯或小人时,杨华得1分;当两张硬纸片上的图形可拼成房子或小山时,季红得1分(如图2).问题:游戏规则对双方公平吗?请说明理由;若你认为不公平,如何修改游戏规则才能使游戏对双方公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,E 为 BC 边中点.
(Ⅰ)已知:如图,若 AE 平分∠BAD,∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD
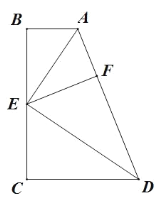
(Ⅱ)已知:如图,若 AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点 F,G 均为 AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+ ![]() BC+CD.
BC+CD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com