Question

17．如图，反比例函数y=$\frac{{k}_{1}}{x}$图象与正比例函数y=k₂x图象相交于点M、N，已知点B（3，3），作BA⊥x轴于A，过点M作MC⊥MN交AB于点C，且$BC=\frac{2}{3}AB$．
（1）求正比例函数和反比例的关系式．
（2）若点P（x，y）是反比例函数图象上的一动点，直接写出当x＞y时x的取值范围．

Answer 1

分析 （1）因为点B在正比例函数的图象上，利用点B的坐标求正比例函数的关系式；
利用△BOA∽△BCM，求出BM的长，则OM=2$\sqrt{2}$，根据△OMD是等腰直角三角形得出点M的坐标，利用待定系数法求出反比例函数的关系式；
（2）分别在两个分支上观察图象得出结论．

解答 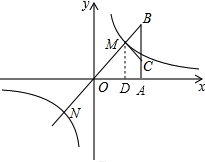解：（1）过M作MD⊥x轴于D，则OB=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$，
把B（3，3）代入y=k₂x中，得3k₂=3，
k₂=1，
∴正比例函数关系式为：y=x；
∵B（3，3），BA⊥x轴，
∴AB=3，
∵$BC=\frac{2}{3}AB$，
∴BC=2，
∵∠OAB=∠CMB=90°，∠B=∠B，
∴△BOA∽△BCM，
∴$\frac{OB}{BC}=\frac{AB}{BM}$，
∴$\frac{3\sqrt{2}}{2}=\frac{3}{BM}$，
∴BM=$\sqrt{2}$，
∴OM=3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$，
∵OA=AB，∠OAB=90°，
∴△OAB是等腰直角三角形，
∴∠BOA=45°，
∴DM=OD，
sin45°=$\frac{DM}{OM}$，
∴DM=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2，
∴M（2，2），
因为点M在反比例函数的图象上，把M（2，2）代入y=$\frac{{k}_{1}}{x}$中得：k₁=2×2=4，
∴反比例函数的关系式为：y=$\frac{4}{x}$；
（2）由对称性得：N（-3，-3），
观察图象得：当x＞0时，x＞3，x＞y；
当x＜0时，-3＜x＜0，x＞y；
∴当x＞y时，-3＜x＜0或x＞3．

点评 本题综合考查了反比例函数与一次函数的性质，掌握运用待定系数法求函数的关系式；在求两函数交点的坐标时，把两个函数关系式联立成方程组求解，如果两函数的关系式未知时，有时会利用相似或勾股定理求点的坐标；对于图象中求某一变量的取值范围，一般采用观察图象得到即可．