解:(1)把B(4,0)代入y=a(x-2)
2+4得:a=-1,
则抛物线L
1:y=-x
2+4x,抛物线L
2:y=x
2+4x;
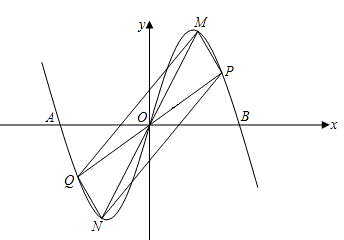
(2)根据P点位置进行分类讨论:
(i)若P点在抛物线的BM段(2<x≤4)时,S
△POM=

+

-

=x
2-2x,
则S
平行四边形PMQN=4S
△POM=4x
2-8x;
(ii)若P点在抛物线的OM段(0<x<2)时,S
△POM=
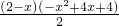
+

-

=-x
2+2x,
则S
平行四边形PMQN=4S
△POM=-4x
2+8x;
(3)当2<x≤4时,y随x的增大而增大,当x=4时,S最大=32,
当0<x<2时,y随x的增大而减小,当x=1时,S最大=4,
∴当x=4时,S最大=32,此时P点坐标为(4,0).
分析:(1)因为函数L
1过点B,所以把点B的坐标代入到L
1的解析式中求出a的值即可得到函数L
1的解析式;由图象绕原点旋转180°可知函数L
1和函数L
2关于原点对称,根据对称的特点即可得到函数L
2的解析式.
(2)由对称性可知四边形PNQM为平行四边形,根据平行四边形的特点可知平行四边形的面积等于三角形POM面积的4倍,分别过M和P作x轴的垂线,交x轴分别为C和D点,然后利用梯形MPDC的面积加上三角形MOC的面积减去三角形POD的面积即可表示出三角形POM的面积,即可得到S与x的关系式;同理,可用梯形PDCM的面积加上三角形OPD的面积减去三角形OMC的面积即可表示出三角形OPM的面积,即可得到S与x的关系式;
(3)当2<x≤4时,y随x的增大而增大,把x代入到(2)求出的S与x的关系式中即可求出S的最大值;又0<x<2时,y随x的增大而减小,把x=1代入到S与x的关系式中即可求出S的最大值,两个最大值比较即可得到最大,然后根据此时的x的值即可得到P的坐标.
点评:此题考查学生会利用待定系数法求函数的解析式,考查了分类讨论的数学思想,掌握二次函数的增减性,是一道综合题.

 +
+ -
- =x2-2x,
=x2-2x,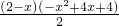 +
+ -
- =-x2+2x,
=-x2+2x,

 阅读快车系列答案
阅读快车系列答案 21、如图,抛物线L1:y=-x2-4x+5交x轴于A、B,交y轴于C,顶点为D
21、如图,抛物线L1:y=-x2-4x+5交x轴于A、B,交y轴于C,顶点为D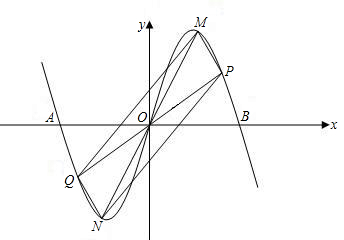
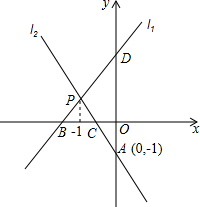 如图,直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).
如图,直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).