
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
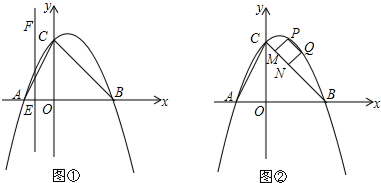
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
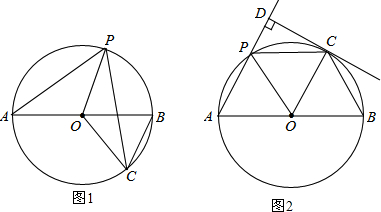
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
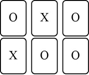 怡君手上有24张卡片,其中12张卡片被画上O记号,另外12张卡片被画上X记号.如图表示怡君从手上拿出6张卡片放在桌面的情形,且她打算从手上剩下的卡片中抽出一张卡片.若怡君手上剩下的每张卡片被抽出的机会相等,则她抽出O记号卡片的机率为何?( )
怡君手上有24张卡片,其中12张卡片被画上O记号,另外12张卡片被画上X记号.如图表示怡君从手上拿出6张卡片放在桌面的情形,且她打算从手上剩下的卡片中抽出一张卡片.若怡君手上剩下的每张卡片被抽出的机会相等,则她抽出O记号卡片的机率为何?( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com