
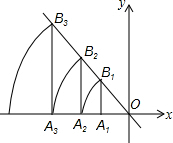
 如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0).
如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0). 分析 先根据一次函数解析式求出B1点的坐标,再根据B1点的坐标求出OA2的长,用同样的方法得出OA3,OA4的长,以此类推,总结规律便可求出点A2016的坐标.
解答  解:∵点A1坐标为(-3,0),
解:∵点A1坐标为(-3,0),
∴OA1=3,
∵在y=-$\frac{4}{3}$x中,当x=-3时,y=4,即B1点的坐标为(-3,4),
∴由勾股定理可得OB1=$\sqrt{{3}^{2}+{4}^{2}}$=5,即OA2=5=3×$\frac{5}{3}$,
同理可得,
OB2=$\frac{25}{3}$,即OA3=$\frac{25}{3}$=5×($\frac{5}{3}$)1,
OB3=$\frac{125}{9}$,即OA4=$\frac{125}{9}$=5×($\frac{5}{3}$)2,
以此类推,
OAn=5×($\frac{5}{3}$)n-2=$\frac{{5}^{n-1}}{{3}^{n-2}}$,
即点An坐标为(-$\frac{{5}^{n-1}}{{3}^{n-2}}$,0),
当n=2016时,点A2016坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0).
故答案为:(-$\frac{{5}^{2015}}{{3}^{2014}}$,0)
点评 本题主要考查了一次函数图象上点的坐标特征以及勾股定理的运用,解题的关键是根据OA1,OA2,OA3,OA4的长总结规律,进而得到OAn的长.解题时注意,直线上任意一点的坐标都满足函数关系式y=kx+b.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:填空题
 为了推动校园足球发展,某市教体局准备向全市中小学免费赠送一批足球,这批足球的生产任务由甲、乙两家足球制造企业平均承担,甲企业库存0.2万个,乙企业库存0.4万个,两企业同时开始生产,且每天生产速度不变,甲、乙两家企业生产的足球数量y万个与生产时间x天之间的函数关系如图所示,则每家企业供应的足球数量a等于1万个.
为了推动校园足球发展,某市教体局准备向全市中小学免费赠送一批足球,这批足球的生产任务由甲、乙两家足球制造企业平均承担,甲企业库存0.2万个,乙企业库存0.4万个,两企业同时开始生产,且每天生产速度不变,甲、乙两家企业生产的足球数量y万个与生产时间x天之间的函数关系如图所示,则每家企业供应的足球数量a等于1万个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
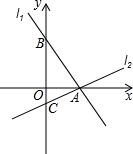 如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.
如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
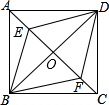 如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是①③④(把所有正确结论的序号都填在横线上)
如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是①③④(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com