
【题目】某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个定价增加x元.
(1)写出售出一个可获得的利润是多少元(用含x的代数式表示)?
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(3)商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少?
【答案】(1)x+10元;(2)每个定价为70元,应进货200个.(3)每个定价为65元时得最大利润,可获得的最大利润是6250元.
【解析】试题分析:(1)根据利润=销售价-进价列关系式,(2)总利润=每个的利润×销售量,销售量为400-10x,列方程求解,根据题意取舍,(3)利用函数的性质求最值.
试题解析:由题意得:(1)50+x-40=x+10(元),
(2)设每个定价增加x元,
列出方程为:(x+10)(400-10x)=6000,解得:x1=10,x2=20,要使进货量较少,则每个定价为70元,应进货200个,
(3)设每个定价增加x元,获得利润为y元,
y=(x+10)(400-10x)=-10x2+300x+4000=-10(x-15)2+6250,当x=15时,y有最大值为6250,所以每个定价为65元时得最大利润,可获得的最大利润是6250元.
【题型】解答题
【结束】
24
【题目】猜想与证明:
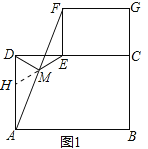
如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.
拓展与延伸:
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
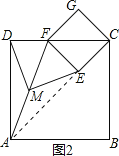
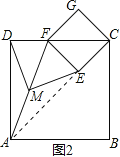
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.

【答案】猜想:DM=ME,证明见解析;(2)成立,证明见解析.
【解析】
试题分析:延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(1)、延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(2)、连接AE,根据正方形的性质得出∠FCE=45°,∠FCA=45°,根据RT△ADF中AM=MF得出DM=AM=MF,根据RT△AEF中AM=MF得出AM=MF=ME,从而说明DM=ME.
试题解析:如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,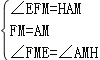
∴△FME≌△AMH(ASA)
∴HM=EM,
在RT△HDE中,HM=DE,
∴DM=HM=ME,
∴DM=ME.
(1)、如图1,延长EM交AD于点H,
∵四边形ABCD和CEFG是矩形,
∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,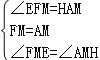
∴△FME≌△AMH(ASA)
∴HM=EM,
在RT△HDE中,HM=EM
∴DM=HM=ME,
∴DM=ME,
(2)、如图2,连接AE,
∵四边形ABCD和ECGF是正方形,
∴∠FCE=45°,∠FCA=45°,
∴AE和EC在同一条直线上,
在RT△ADF中,AM=MF,
∴DM=AM=MF,
在RT△AEF中,AM=MF,
∴AM=MF=ME,
∴DM=ME.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】小李对初三(1)班全体同学的业余兴趣爱好(第一爱好)进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.

请你根据图中提供的信息,解答下列问题:
(1)初三(1)班共有学生________人;
(2)在图1中,将“书画”部分的图形补充完整;
(3)在图2中,“球类”部分所对应的圆心角的度数________度;爱好“音乐”的人数占本班学生数的百分数是________;爱好“书画”的人数占本班学生数的百分数是________;“其它”的人数占本班学生数的百分数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,连接
上一点,连接![]() 交对角线
交对角线![]() 于点
于点![]() .
.
(1)如图1,已知![]() 于
于![]() ,菱形的边长为6,求线段
,菱形的边长为6,求线段![]() 的长度;
的长度;
(2)如图2,已知点![]() 为边
为边![]() 上一点,连接
上一点,连接![]() 交线段
交线段![]() 于点
于点![]() ,且满足
,且满足![]() ,
,![]() ,求证:
,求证:![]() .
.
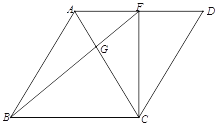
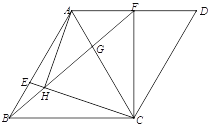
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
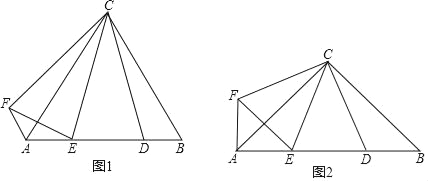
【题目】(1)操究发现:如图1,△ABC为等边三角形,点D为AB边上的一点,∠DCE=30°,∠DCF=60°且CF=CD
①求∠EAF的度数;
②DE与EF相等吗?请说明理由
(2)类比探究:如图2,△ABC为等腰直角三角形,∠ACB=90°,点D为AB边上的一点,∠DCE=45°,CF=CD,CF⊥CD,请直接写出下列结果:
①∠EAF的度数
②线段AE,ED,DB之间的数量关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
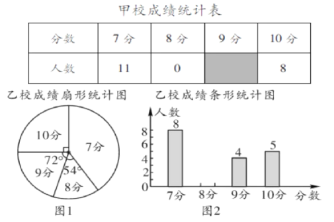
(1)在图1中,“7分”所在扇形的圆心角等于 .
(2)请你将图2的条形统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+1的图象与反比例函数y=![]() 的图象在第一象限相交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C,如果四边形OBAC是正方形.
的图象在第一象限相交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C,如果四边形OBAC是正方形.
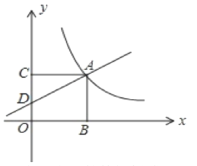
(1)求一次函数的解析式。
(2)一次函数的图象与y轴交于点D. 在x轴上是否存在一点P,使得PA+PD最小?若存在,请求出P点坐标及最小值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为: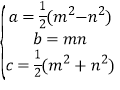 其中m>n>0,m,n是互质的奇数.
其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
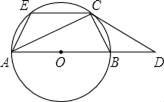
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,过C点的切线与AB的延长线交于点D,CE∥AB交⊙O于点E,连接AC、BC、AE.
(1)求证:①∠DCB=∠CAB;②CDCE=CBCA;
(2)作CG⊥AB于点G.若tan∠CAB=![]() (k>1),求
(k>1),求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点A(0,2)和点B(4,2)都在二次函数y=x2+bx+c的图象上,那么此抛物线在直线_____的部分是上升的.(填具体某直线的某侧)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com