
 如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$.
如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$. 分析 先证得∠GED=∠CDF,然后利用两角法判断△EGD∽△DCF,设点E坐标为(k,1),点F坐标为(2,$\frac{k}{2}$),即可得CF=$\frac{k}{2}$,BF=DF=1-$\frac{k}{2}$,在Rt△CDF中表示出CD,利用对应边成比例可求出k的值.
解答 解:由折叠的性质可得:BE=DE,BF=DF,∠B=∠EDF=90°,
∵∠CDF+∠EDG=90°,∠GED+∠EDG=90°,
∴∠CDF=∠GED,
又∵∠EGD=∠DCF=90°,
∴△EGD∽△DCF,
设点E坐标为(k,1),点F坐标为(2,$\frac{k}{2}$),
则CF=$\frac{k}{2}$,BF=DF=1-$\frac{k}{2}$,ED=BE=AB-AE=2-k,
在Rt△CDF中,CD=$\sqrt{D{F}^{2}-C{F}^{2}}$=$\sqrt{(1-\frac{k}{2})^{2}-(\frac{k}{2})^{2}}$=$\sqrt{1-k}$,
∵$\frac{CD}{GE}$=$\frac{DF}{ED}$,即$\frac{\sqrt{1-k}}{1}$=$\frac{1-\frac{k}{2}}{2-k}$,
∴$\sqrt{1-k}$=$\frac{1}{2}$,
解得:k=$\frac{3}{4}$.
故答案为$\frac{3}{4}$.
点评 本题考查了反比例函数的综合,解答本题的关键是利用点E的纵坐标,点F的横坐标,用含k的式子表示出其他各点的坐标,注意掌握相似三角形的对应边成比例的性质,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在所建立的平面直角坐标系中:
在所建立的平面直角坐标系中:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
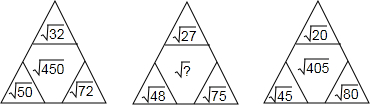
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com