
 在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.分析 (1)由四边形ABCD是矩形,可得∠BAD=∠BCD=90°,AB=CD,AB∥CD,又由折叠的性质可得:∠EBD=$\frac{1}{2}$∠ABD,∠FDB=$\frac{1}{2}$∠CBD,即可证得BE∥DF,然后由DE∥BF,即可证得四边形BFDE为平行四边形.
(2)首先由菱形与矩形的性质,求出∠ABE=30°,根据直角三角形性质求出AE、BE,即可求出答案.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠BAD=∠BCD=90°,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
由折叠的性质可得:∠EBD=$\frac{1}{2}$∠ABD,∠FDB=$\frac{1}{2}$∠CBD,
∴∠EBD=∠FDB,
∴EB∥DF,
∵ED∥BF,
∴四边形BFDE为平行四边形.
(2)解:∵四边形BFDE为菱形,
∴BE=ED,∠EBD=∠FBD=∠ABE,
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=90°,
∴∠ABE=30°,
∵∠A=90°,AB=1,
∴AE=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,BE=2AE=$\frac{2\sqrt{3}}{3}$,
∴BC=AD=AE+ED=AE+BE=$\frac{\sqrt{3}}{3}$+$\frac{2\sqrt{3}}{3}$=$\sqrt{3}$.
点评 本题考查了平行四边形的判定,菱形的性质,矩形的性质,含30度角的直角三角形性质的应用,注意折叠中的对应关系.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
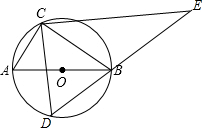 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )| A. | 2$\sqrt{5}$ | B. | 5$\sqrt{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )| A. | 一直减小 | B. | 先减小后增大 | C. | 一直增大 | D. | 先增大后减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.
在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.| P从O出发的时间 | 可以得到的整点的坐标 | 可以得到的整点的个数 |
| 1秒 | (0,1)、(1,0) | 2个 |
| 2秒 | (2,0)、(0,2)、(1,1) | 3 |
| 3秒 | (3,0)、(0,3)、(1,2)、(2,1) | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将长方形纸片ABCD折叠,使点D与点B重合,折痕为EF.已知AB=6cm,BC=18cm,则Rt△ABE的面积为( )
如图,将长方形纸片ABCD折叠,使点D与点B重合,折痕为EF.已知AB=6cm,BC=18cm,则Rt△ABE的面积为( )| A. | 27cm2 | B. | 24cm2 | C. | 22cm2 | D. | 20cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,以△ABC的边AB作直径的⊙O,分别交AC、BC于点D、E,弦FG∥AB,S△CDE:S△ABC=1:4,DE=5cm,FG=8cm,求梯形AFGB的面积.
已知,如图,以△ABC的边AB作直径的⊙O,分别交AC、BC于点D、E,弦FG∥AB,S△CDE:S△ABC=1:4,DE=5cm,FG=8cm,求梯形AFGB的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
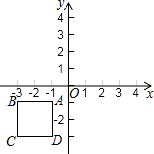 如图,在直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1).我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”称为一次变换.若正方形ABCD经过2015次这样的变换得到正方形A2015B2015C2015D2015,则点B2015的坐标是(4027,1).
如图,在直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1).我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”称为一次变换.若正方形ABCD经过2015次这样的变换得到正方形A2015B2015C2015D2015,则点B2015的坐标是(4027,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com