
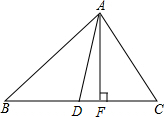
 如图在△ABC中,∠BAD=∠CAD,∠C>∠B,AF⊥BC于点F.求证:∠DAF=$\frac{1}{2}$(∠C-∠B).
如图在△ABC中,∠BAD=∠CAD,∠C>∠B,AF⊥BC于点F.求证:∠DAF=$\frac{1}{2}$(∠C-∠B). 分析 首先根据三角形的内角和定理和角平分线的定义表示∠DAC=$\frac{1}{2}$(180°-∠B-∠C),然后根据三角形的内角和定理及等式的性质表示出∠FAD,最后根据等量代换即可得证.
解答  证明:∵AD平分∠BAC(已知),
证明:∵AD平分∠BAC(已知),
∴∠DAC=$\frac{1}{2}$∠BAC(角平分线定义).
∵∠BAC+∠B+∠C=180°(三角形三个内角的和等于180°),
∴∠BAC=180°-∠B-∠C(等式性质).
∴∠DAC=$\frac{1}{2}$(180°-∠B-∠C)(等量代换).
∵AF⊥BC(已知),
∴∠AFC=90°(垂直定义).
在△AFC中,∠AFC+∠C+∠FAC=180°(三角形三个内角的和等于180°),
∴∠FAC=180°-∠AFC-∠C(等式性质)=90°-∠C.
∴∠FAD=∠DAC-∠FAC
=$\frac{1}{2}$(180°-∠B-∠C)-(90°-∠C)
=$\frac{1}{2}$(180°-∠B-∠C)-$\frac{1}{2}$(180°-2∠C)
=$\frac{1}{2}$(180°-∠B-∠C-180°+2∠C)
=$\frac{1}{2}$(∠C-∠B).
点评 本题主要考查了三角形的内角和定理、角平分线的定义、垂直的定义等知识.解决问题的关键是运用三角形内角和定理以及角的和差关系进行计算.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
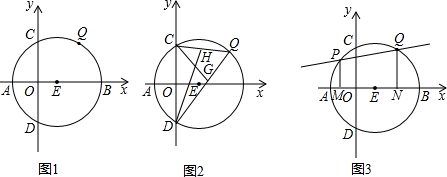
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
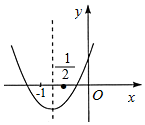 二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c-b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c-b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
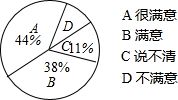 某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有14名.
某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有14名.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠B>45° | B. | ∠A与∠B互余 | ||
| C. | ∠C=90° | D. | △ABC为直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com