
【题目】如图,抛物线![]() 的顶点为B(1,3),与
的顶点为B(1,3),与![]() 轴的交点A在点 (2,0)和(3,0)之间.以下结论:
轴的交点A在点 (2,0)和(3,0)之间.以下结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ≥
≥![]() ;⑤若
;⑤若![]() ,且
,且![]() ,
,
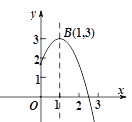
则![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
【解析】由已知可知抛物线的对称轴为:x=1,a<0,c>0,
因为与x轴的一个交点在点(2,0)和(3,0)之间,所以与x轴的另一个交点在(-1,0)和(0,0)之间,
∵a<0, ![]() ,∴b>0,∴abc<0,故①错误;
,∴b>0,∴abc<0,故①错误;
∵抛物线开口向下,与x轴的一个交点在点(2,0)和(3,0)之间,另一个交点在(-1,0)和(0,0)之间,
∴x=-1时,y=a-b+c<0,故②正确;
∵对称轴为x=-![]() ,∴b=-2a,∴2a+b=0,故③正确;
,∴b=-2a,∴2a+b=0,故③正确;
∵抛物线的顶点(1,3),∴a+b+c=3为最大值,
∴a+b+c≥am2+bm+c,即a+b≥am2+bm,故④正确;
∵![]() ,且
,且![]() ,
,
∴![]() +c
+c![]() +c,
+c,
∴x1+x2=2,故⑤正确,
故选A.


科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若 1 表示的点与﹣1 表示的点重合,则﹣2 表示的点与数______表示的点重合;
(2)若﹣1 表示的点与 3 表示的点重合,
①那么 7 表示的点与数_______表示的点重合;
②若数轴上 A、B 两点之间的距离为 11(点 A 在点 B 的左侧),且 A、B 两点经折叠之后 重合,求 A、B 两点表示的数是多少.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校七年级某班准备买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副![]() 元,乒乓球每盒
元,乒乓球每盒![]() 元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的
元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的![]() 折优惠这个班级需要球拍
折优惠这个班级需要球拍![]() 副,乒乓球
副,乒乓球![]() 盒(
盒(![]() ).
).
(1)分别求甲、乙两家商店购买这些商品所箭的费用(用含x的代数式表示);
(2)当![]() 时,购买所需商品去哪家商店合算?请通过计算说明理由.
时,购买所需商品去哪家商店合算?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
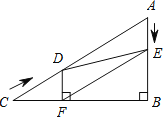
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
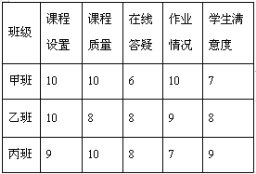
【题目】受疫情影响,某地无法按原计划正常开学.在延迟开学期间该地区组织了在线教学活动.开学后,某校针对各班在线教学的个性化落实情况,通过初评决定从甲、乙、丙三个班中推荐一个作为在线教学先进班级,下表是这三个班的五项指标的考评得分表(单位:分):
根据统计表中的信息解答下列问题:
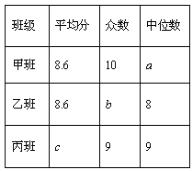
(1)请确定如下的“五项指标的考评得分分析表”中的a、b、c的值:
(2)如果学校把“课程设置”、“课程质量”、“在线答疑”、“作业情况”、“学生满意度”这五项指标得分按照2∶2∶3∶1∶2的比例确定最终成绩,请你通过计算判断应推荐哪个班为在线教学先进班级?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,若一个点到一条直线的距离不大于1,则 称这个点是该直线的“邻点”.在平面直角坐标系中,已知点![]()
![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() 平行于
平行于![]() 轴,并将
轴,并将![]() 进行平移,平移后点
进行平移,平移后点![]() 分别对应点
分别对应点![]() .
.
(1)点![]() (填写是或不是)直线
(填写是或不是)直线![]() 的“邻点”,请说明理由;
的“邻点”,请说明理由;
(2)若点![]() 刚好落在直线
刚好落在直线![]() 上,点
上,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 落在
落在![]() 轴上,且
轴上,且![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标,判断点
的坐标,判断点![]() 是否是直线
是否是直线![]() 的“邻点”,并说明理由.
的“邻点”,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
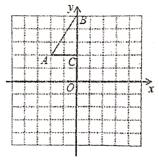
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度.![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() .
.
(1)将![]() 以点
以点![]() 为旋转中心旋转
为旋转中心旋转![]() ,得到
,得到![]() ,请画出
,请画出![]() 的图形.
的图形.
(2)将![]() 以
以![]() 为旋转中心,逆时针旋转
为旋转中心,逆时针旋转![]() ,得到
,得到![]() ,请画出
,请画出![]() 的图形.
的图形.
(3)线段![]() 的长度为______.
的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线经过点 A (-2,0)、 B (4,0)、 C (0,-8),抛物线 y = a x 2 + b x + c (a≠0)与直线 y = x -4交于 B , D 两点.

(1)求抛物线的解析式并直接写出 D 点的坐标;
(2)点 P 为抛物线上的一个动点,且在直线 BD 下方,试求出△ BDP 面积的最大值及此时点 P 的坐标;
(3)点 Q 是线段 BD 上异于 B 、 D 的动点,过点 Q 作 QF ⊥ x 轴于点 F , 交抛物线于点 G . 当△ QDG 为直角三角形时,求点 Q 的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com