
分析 设两直角边为x、y,则斜边为20-(x+y),根据已知得:$\frac{1}{2}$xy=10,即xy=20,由勾股定理求出x2+y2,从而求出斜边长.
解答 解:设两直角边为x、y,则斜边为20-(x+y),
根据已知得:$\frac{1}{2}$xy=10,即xy=20,
由勾股定理得:
x2+y2=[20-(x+y)]2,
x2+y2=400-40(x+y)+(x+y)2,
x2+y2=400-40(x+y)+x2+y2+2xy,
x+y=11,
(x+y)2=121,
x2+y2=81,
∴$\sqrt{{x}^{2}+{y}^{2}}$=9,
即斜边长为9.
点评 本题考查了勾股定理的应用.此题运用三角形面积表示出xy=20,然后由勾股定理导出x2+y2是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
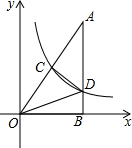 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=18,则S△OBD的值为12.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=18,则S△OBD的值为12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
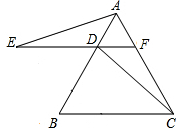 如图,△ABC是等边三角形,过AB上的一点D作DF∥BC,交AC于F,在FD的延长线上取点E,使DE=DB,连接AE、CD.证明:△AFE≌△DAC.
如图,△ABC是等边三角形,过AB上的一点D作DF∥BC,交AC于F,在FD的延长线上取点E,使DE=DB,连接AE、CD.证明:△AFE≌△DAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
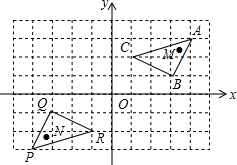 如图,△PQR是三角形ABC经过某种变换后得到的图形.
如图,△PQR是三角形ABC经过某种变换后得到的图形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com