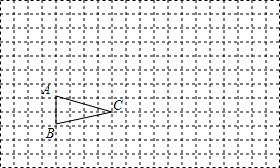
作图题:如图所示.△ABC在方格纸中(1)请在方格纸上建立平面直角坐标系.使A.并求出B点坐标,(2)以原点O为位似中心.相似比为2.在第一象限内将△ABC放大.画出放大后的图形△A′B′C′．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

9．

作图题：如图所示，△ABC在方格纸中
（1）请在方格纸上建立平面直角坐标系，使A（2，3），C（6，2），并求出B点坐标；
（2）以原点O为位似中心，相似比为2，在第一象限内将△ABC放大，画出放大后的图形△A′B′C′．

分析（1）利用A，B点坐标，进而得出原点位置，进而得出B点坐标；
（2）利用位似图形的性质得出对应点位置进而得出答案．

解答解：（1）如图所示：B（2，1）；

（2）如图所示：△A′B′C′，即为所求．

点评此题主要考查了位似变换，根据题意得出对应点位置是解题关键．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

3．某市居民生活用水实行“阶梯水价”收费，具体收费标准件下表：

每户每月用水量	水费价格（单位：元/吨）
不超过20	1.65
超过20吨且不超过30吨的部分	2.48
超过30吨的部分	3.3

例：甲用户1月份用水25吨，应缴水费1.65×20+2.48×（25-20）=45.4（元）．
（1）若乙用户1月份用水10吨，则应缴水费16.5元；
（2）若丙用户1月份应缴水费64.4元，则用水32吨；
（3）用丁用户1、2两个月共用水60吨，（1月份用水量超过了2月份），设2月份用水a吨，求丁用户1、2月份各应缴水费多少元？（用含a的代数式表示）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．已知关于x的方程x²-（2k+1）x+4（k-$\frac{1}{2}$）=0
（1）求证：无论k取何值，这个方程总有实数根；
（2）若等腰三角形ABC的一边长a=4，另两边b、c恰好是这个方程的两个根，求△ABC的周长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．下列函数中，哪些是y关于x的二次函数？
①y=x²+$\frac{1}{x}$；②y=2x（3-x）；③y=-$\frac{1}{2}$x-$\sqrt{3}$x²；④y=ax²+bx+c；⑤y=（a²+1）x²+5x-3；⑥y=2x²-x（1+2x-5x²）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．

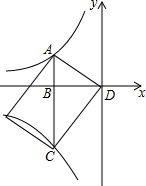如图，点A是反比例函数y₁=$\frac{k}{x}$（k＜0，x＜0）的图象上的任意一点，过点A作AB⊥x轴于点B，并延长交另一个反比例函数y₂=$\frac{12}{x}$（x＜0）的图象于点C，连接OC，S_△AOB=3．
（1）求k的值；
（2）若点A的横坐标是-3；则反比例函数y₂=$\frac{12}{x}$的图象上是否存在点D，使四边形AOCD是平行四边形？若存在，请求出点D的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

14．

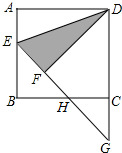如图，点E是正方形ABCD的边AB上一点，且∠ADE=22.5°，将△ADE沿DE翻折得到△FDE，延长EF交BC于点H，交DC的延长线于点G，则图中所有的等腰三角形是△EBH、△GHC、△EDG（将符合条件的所有三角形全部列举出来）．