
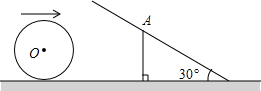
 如图,桌面上有一半径为r小球向右滚动,前面有一块与桌面垂直的垂直挡板AC和一块与桌面成30°角B的斜挡板AB,两块挡板相交于点A,且有一端都紧靠桌面,如果AC=2.
如图,桌面上有一半径为r小球向右滚动,前面有一块与桌面垂直的垂直挡板AC和一块与桌面成30°角B的斜挡板AB,两块挡板相交于点A,且有一端都紧靠桌面,如果AC=2. 分析 设当小球到O'位置时,与AC撞击,作O'E⊥AC交AB于点F,作O'D⊥AB于点D.则O'E=r,AE=2-r.三角函数r表示出O'D的长度.
(1)当r=1.2时求得O'D的长度,只要小于1.2就是先撞击AC;
(2)当O'D=r时,球同时撞击两块挡板,据此列方程求解;
当O'D<r时,球同时撞击两块挡板,列不等式即可求解.
解答 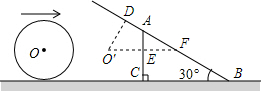 解:设当小球到O'位置时,与AC撞击,作O'E⊥AC交AB于点F,作O'D⊥AB于点D.
解:设当小球到O'位置时,与AC撞击,作O'E⊥AC交AB于点F,作O'D⊥AB于点D.
则O'E=r,AE=2-r.
在直角△AEF中,∠AFE=∠ABC=30°,
则EF=$\sqrt{3}$AE=$\sqrt{3}$(2-r).O'F=r+EF=$\sqrt{3}$(2-r)+r.
则O'D=$\frac{1}{2}$O'F=$\sqrt{3}$-$\frac{1}{2}$($\sqrt{3}$-1)r.
(1)当r=1.2时,O'D=$\sqrt{3}$-$\frac{1}{2}$($\sqrt{3}$-1)×1.2=$\frac{2\sqrt{3}}{5}$+0.6>1.2,则当当r=1.2时,试说明球必先撞击竖直挡板AC;
(2)当O'D=r时,球同时撞击两块挡板,则$\sqrt{3}$-$\frac{1}{2}$($\sqrt{3}$-1)r=r,
解得:r=2;
当O'D<r时,球同时撞击两块挡板,则$\sqrt{3}$-$\frac{1}{2}$($\sqrt{3}$-1)r<r,
解得:r>2.
故答案是:=2;>2.
点评 本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | S=60x | B. | S=x(60-x) | C. | S=x(30-x) | D. | S=30x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
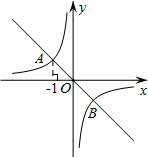 已知:如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=-$\frac{1}{x}$的图象交于A、B两点.
已知:如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=-$\frac{1}{x}$的图象交于A、B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com