Question

【题目】某水果大卖场每日批量进货销售某种水果，假设日销售量与日进货量相等．设该水果进货量为x千克，每千克进货成本为y元，每千克售价为s元，y与x的关系如图，s与x满足关系式：s=﹣ x+12．

（1）请解释图中线段BC的实际意义；
（2）该水果进货量为多少时，获得的日销售利润最大？最大利润是多少？

Answer 1

【答案】
（1）解：图中线段BC表示当进货量80≤x≤120时，每千克的进货成本y=4元
（2）解：设AB所在直线解析式为：y=kx+b，

由题意得： ，

解得： ，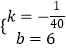

故当0＜x＜80时，y=﹣ x+6，

设获得的日销售利润为W，根据题意，

①当0＜x＜80时，

W=[（﹣ x+12）﹣（﹣ x+6）]x

=﹣ x2+6x

=﹣ （x﹣72）2+216，

当x=72时，W最大值=216；

②当80≤x≤120时，

W═（﹣ x+12﹣4）x

=﹣ x2+8x

=﹣ （x﹣60）2+240，

当x＞60时，W随x的增大而减小，

故当x=80时，W最大值= ，

∵216＞ ，

∴当水果进货量为72千克时，获得的日销售利润最大，最大利润是216元

【解析】（1）图中线段BC表示当进货量80≤x≤120时，每千克的进货成本均为4元；（2）根据“获得的日销售利润=每千克的利润×进货量”分0＜x＜80和80≤x≤120列出函数关系式，求最大值，比较后可得．