Question

（2013•江西）某学校活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
●操作发现：
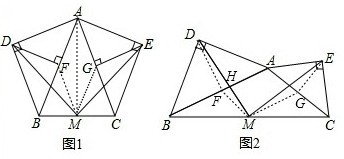
在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是

①②③④

（填序号即可）
①AF=AG=

1

2

AB；②MD=ME；③整个图形是轴对称图形；④∠DAB=∠DMB．
●数学思考：
在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD与ME具有怎样的数量和位置关系？请给出证明过程；
●类比探究：
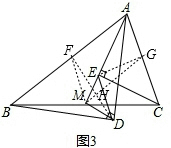
在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．答：

等腰直角三角形

．

Answer 1

分析：操作发现：由条件可以通过三角形全等和轴对称的性质，直角三角形的性质就可以得出结论；
数学思考：作AB、AC的中点F、G，连接DF，MF，EG，MG，根据三角形的中位线的性质和等腰直角三角形的性质就可以得出四边形AFMG是平行四边形，从而得出△DFM≌△MGE，根据其性质就可以得出结论；
类比探究：作AB、AC的中点F、G，连接DF，MF，EG，MG，DF和MG相交于H，根据三角形的中位线的性质K可以得出△DFM≌△MGE，由全等三角形的性质就可以得出结论；

解答：解：●操作发现：
∵△ADB和△AEC是等腰直角三角形，
∴∠ABD=∠DAB=∠ACE=∠EAC=45°，∠ADB=∠AEC=90°
在△ADB和△AEC中，

∠ADB=∠AEC ∠ABD=∠ACE AB=AC

，
∴△ADB≌△AEC（AAS），
∴BD=CE，AD=AE，
∵DF⊥AB于点F，EG⊥AC于点G，
∴AF=BF=DF=

1

2

AB，AG=GC=GE=

1

2

AC．
∵AB=AC，
∴AF=AG=

1

2

AB，故①正确；
∵M是BC的中点，
∴BM=CM．
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABC+∠ABD=∠ACB+∠ACE，
即∠DBM=∠ECM．
在△DBM和△ECM中，

BD=CE ∠DBM=∠ECM BM=CM

∴△DBM≌△ECM（SAS），
∴MD=ME．故②正确；
连接AM，根据前面的证明可以得出将图形1，沿AM对折左右两部分能完全重合，
∴整个图形是轴对称图形，故③正确．
∵AB=AC，BM=CM，
∴AM⊥BC，
∴∠AMB=∠AMC=90°，
∵∠ADB=90°，
∴四边形ADBM四点共圆，
∴∠AMD=∠ABD=45°．
∵AM是对称轴，
∴∠AME=∠AMD=45°，
∴∠DME=90°，
∴MD⊥ME，故④正确，
故答案为：①②③④

●数学思考：
MD=ME，MD⊥ME．
理由：作AB、AC的中点F、G，连接DF，MF，EG，MG，
∴AF=

1

2

AB，AG=

1

2

AC．
∵△ABD和△AEC是等腰直角三角形，
∴DF⊥AB，DF=

1

2

AB，EG⊥AC，EG=

1

2

AC，
∴∠AFD=∠AGE=90°，DF=AF，GE=AG．
∵M是BC的中点，
∴MF∥AC，MG∥AB，
∴四边形AFMG是平行四边形，
∴AG=MF，MG=AF，∠AFM=∠AGM．
∴MF=GE，DF=MG，∠AFM+∠AFD=∠AGM+∠AGE，
∴∠DFM=∠MGE．
在△DFM和△MGE中，

FM=GE ∠DFM=∠MGE DF=MG

，
∴△DFM≌△MGE（SAS），
∴DM=ME，∠FDM=∠GME．
∵MG∥AB，
∴∠GMH=∠BHM．
∵∠BHM=90°+∠FDM，
∴∠BHM=90°+∠GME，
∵∠BHM=∠DME+∠GME，
∴∠DME+∠GME=90°+∠GME，
即∠DME=90°，
∴MD⊥ME．
∴DM=ME，MD⊥ME；

●类比探究：
∵点M、F、G分别是BC、AB、AC的中点，
∴MF∥AC，MF=

1

2

AC，MG∥AB，MG=

1

2

AB，
∴四边形MFAG是平行四边形，
∴MG=AF，MF=AG．∠AFM=∠AGM
∵△ADB和△AEC是等腰直角三角形，
∴DF=AF，GE=AG，∠AFD=∠BFD=∠AGE=90°
∴MF=EG，DF=MG，∠AFM-∠AFD=∠AGM-∠AGE，
即∠DFM=∠MGE．
在△DFM和△MGE中，

FM=GE ∠DFM=∠MGE DF=MG

，
∴△DFM≌△MGE（SAS），
∴MD=ME，∠MDF=∠EMG．
∵MG∥AB，
∴∠MHD=∠BFD=90°，
∴∠HMD+∠MDF=90°，
∴∠HMD+∠EMG=90°，
即∠DME=90°，
∴△DME为等腰直角三角形．

点评：本题考查了等腰直角三角形的性质的运用，等腰三角形的性质的运用，全等三角形的判定及性质的运用，三角形的中位线的性质的运用，直角三角形的斜边上的中线的性质的运用，平行四边形的判定及性质的运用，解答时根据三角形的中位线的性质制造全等三角形是解答本题的关键．