
【题目】如今,优学派电子书包通过将信息技术与传统教学深度结合,让智能科技在现代教育中发挥了重要作用。某优学派公司筹集资金12.8万元,一次性购进两种新型电子书包访问智能终端:平板电脑和PC机共30台.根据市场需要,这些平板电脑、PC机可以全部销售,全部销售后利润不少于1.5万元,其中平板电脑、PC机的进价和售价见如下表格:

设该公司计划购进平板电脑x台,平板电脑和PC机全部销售后该公司获得的利润为y元.
(1) 试写出y与x的函数关系式;
(2) 该公司有哪几种进货方案可供选择?请写出具体方案;
(3) 选择哪种进货方案,该公司获利最大?最大利润是多少元?
【答案】(1)y= 300x+12000;(2)见解析;(3)购进平板电脑12台,PC机18台。能获得最大利润是15600元.
【解析】试题分析:(1)设该公司计划购进平板电脑x台,则购进PC机(30-x)台,根据题意可得等量关系:公司获得的利润y=平板电脑x台的利润+PC机(30-x)台的利润,根据等量关系可得函数关系式;
(2)根据资金12.8万元和利润不少于1.5万元列出不等式组,解不等式组即可;
(3) 根据一次函数的性质:k>0时,y随x的增大而增大可得答案.
试题解析:
(1)设该公司计划购进平板电脑x台,则购进PC机(30-x)台,
根据题意得:y=(6100﹣5400)x+(3900﹣3500)(30﹣x) ,整理得:y= 300x+12000;
(2)由题意得: ![]() , 解之得:
, 解之得: ![]() ,
,
∴整数x=10,11,或12 ;
所以该公司共有3种进货方案可供选择:
方案一:购进平板电脑10台,PC机20台;
方案二:购进平板电脑11台,PC机19台;
方案三:购进平板电脑12台,PC机18台;
(3)∵对于函数y= 300x+12000,y随x的增大而增大,
∴该公司选择方案三:购进平板电脑12台,PC机18台。能获得最大利润,
此时,最大利润y= 300×12+12000=15600 (元).


科目:初中数学 来源: 题型:
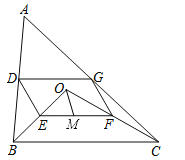
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2﹣10x+21=0的两根恰好是等腰三角形的底边长和腰长,则该等腰三角形的周长为( )
A. 13B. 17C. 13或17D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com